const_missing 有没有实例，求分享。

建议挂在其他节点

最近在读元编程第二版，贴一个元编程的例子

class Algo
  def method_missing(method_name,*args)
    op="*" if method_name==:multiply
    op="+" if method_name==:add ## method name is a symbol
    op="/" if method_name==:divide
    op="-" if method_name==:minus
    super.method_missing(method_name,*args) if not op
    args.inject(:"#{op}")
  end
end

obj=Algo.new
p obj.add(1,2,3,4)
p obj.multiply(1,2,3,4)
p obj.take(1,2,3,4)

直白明了！谢谢作者

#28 楼 @nouse 一个更好的解法（注意：题目需求已变）

def group_anagrams(strs)
    strs.group_by{|str| str.chars.sort}.values.map(&:sort)    
end

#11 楼 @msg7086 这段代码看起来有些乱。。。

#10 楼 @msg7086 代码很清爽

#4 楼 @luikore 跑了一下，C 下 0ms

#3 楼 @luikore 恩，这种使用 O(n) 空间的做法会让代码非常简洁。我用过循环赋值的方法，那样代码要累赘一点，但只用 O(1) 空间。各有优缺。

#5 楼 @kewin 10.9.

#1 楼 @luikore 恩，刚开始时还习惯用 java 的路数。。

#19 楼 @yakczh leetcode 中有这道题，你可以在我的 github 中找。欢迎围观我发表的那个刷题帖。

#29 楼 @alvin2ye 根本就是错的。这个是浅复制。

使用回溯法。dfs 即可。很简单，帮楼主写了一个。试试看。

def sum_array_equals_to(target)
  elements=[]
  target.times{|i| elements<<i+1}
  result=[]
  dfs(target,0,[],elements,result)
  result.uniq
end

def dfs(target,curSum,curArray,elements,result)
  result<<curArray.sort if target==curSum
  elements.each do |e|
    if curSum+e<=target
      elements-=[e]
      dfs(target,curSum+e,curArray+[e],elements,result)
      elements+=[e]
    end
  end
end
p sum_array_equals_to(6)

#3 楼 @quakewang 受你启发，我重写了 two sum。最多遍历数组一次。而且无需对数组排序。同时，按序遍历保证会将结果按序输出。代码如下。总共 4 行，68ms。

def two_sum(nums,target)
  hash=Hash.new
  nums.each_with_index {|n,i| return [hash[n],i+1] if hash[n]!=nil; hash[target-n]=i+1 }
end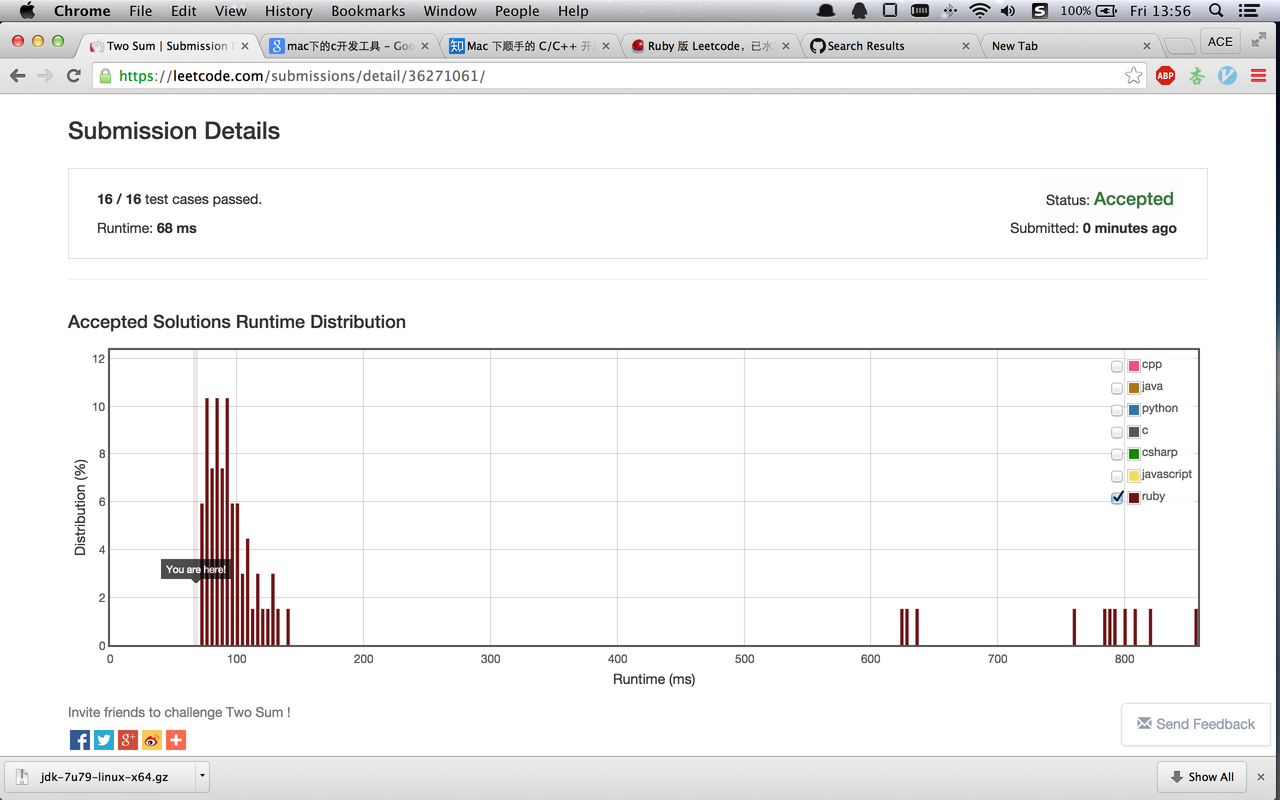

顺便发个图正确多待一会首页。

入门好贴！

#15 楼 @h_minghe 好，多交流。

#13 楼 @h_minghe https://github.com/acearth/LeetCodePractice/

https://ruby-china.org/topics/26529

#24 楼 @quakewang 这么做确实更快，我的耗时 192ms

贴一个数字转罗马数的代码

def int_to_roman(num)
  dfs(num,"")
end
def dfs(val,tmpStr)
  case val
  when 1000..3999 then dfs(val-1000,tmpStr+'M')
  when 900..999 then dfs(val-900,tmpStr+'CM')
  when 500..899 then dfs(val-500,tmpStr+'D')
  when 400..499 then dfs(val-400,tmpStr+'CD')
  when 100..399 then dfs(val-100,tmpStr+'C')
  when 90..99 then dfs(val-90,tmpStr+'XC')
  when 50..89 then dfs(val-50,tmpStr+'L')
  when 40..49 then dfs(val-40,tmpStr+'XL')
  when 10..39 then dfs(val-10,tmpStr+'X')
  when 9 then return tmpStr+'IX'
  when 5..8 then dfs(val-5,tmpStr+'V')
  when 4 then return tmpStr+'IV'
  when 1..3 then dfs(val-1,tmpStr+'I')
  when 0  then tmpStr
  end
end

p int_to_roman 1
p int_to_roman 1999
p int_to_roman 1880

这个题可以把 4*，9的情况并入到 5##，1**的情况里，但是会引入不必要的代码。有朋友说 case 太多了，该怎么优化

代码地址 https://github.com/acearth/LeetCodePractice/blob/master/int_to_roman_dfs.rb

#16 楼 @cicholgricenchos 具体是哪一题？贴出来看看

#13 楼 @seaify 主要是为了给应聘吃个定心丸。感觉用 ruby 写算法题，不用考虑 c/c++ 的很多语法坑，这是 ruby 的优势。另，我好像暴露了。

#3 楼 @quakewang 涨姿势了！

#6 楼 @quakewang factorial trailing zero 用 inject 最快，做这题要利用遇 5 添 0 的阶乘性质，用 inject 体现了这种思想。但求素数，如果直接用内置对象，那题目是能做出来，但违背了做题的目的。这里我只能看到你熟悉 prime 对象，却难以知晓你是否会求解。

#5 楼 @quakewang 感谢@quakewang 指正，我写 ruby 纯属自娱自乐，往往不清楚某一块是写的好还是烂。现在有了镜子，终于可以打磨代码了。

#1 楼 @msg7086 恩，查了一下，改变流程更常用 catch throw。

@deathking a 题用 ruby 毫无压力。你真的用 ruby 做过题吗、

@h_minghe 可移步我的帖子，互相学习。

很有用，mark 下以后看