Ruby 几道有趣的 leetcode 题目

arth · 2015年08月19日 · 最后由 torubylist 回复于 2016年01月13日 · 4293 次阅读

今天刚刚做完第 200 道 leetcode 题目。说说自己的感受，并分享两道有趣的题目。

1.运行时间排名只有相同语言的排名才有意义。我原先以为 ruby 比 python 快，有时确实如此，但也不确定。前几天看了个 leetcode 的 discuss 帖子，说某题用 python 比 C++ 要快很多----都知道 C、C++ 在时间排名上一般总高于其他语言。系统管理员 1337coder 的回复大概是与机器等配置有关，用户不宜以此和其他语言做对比。

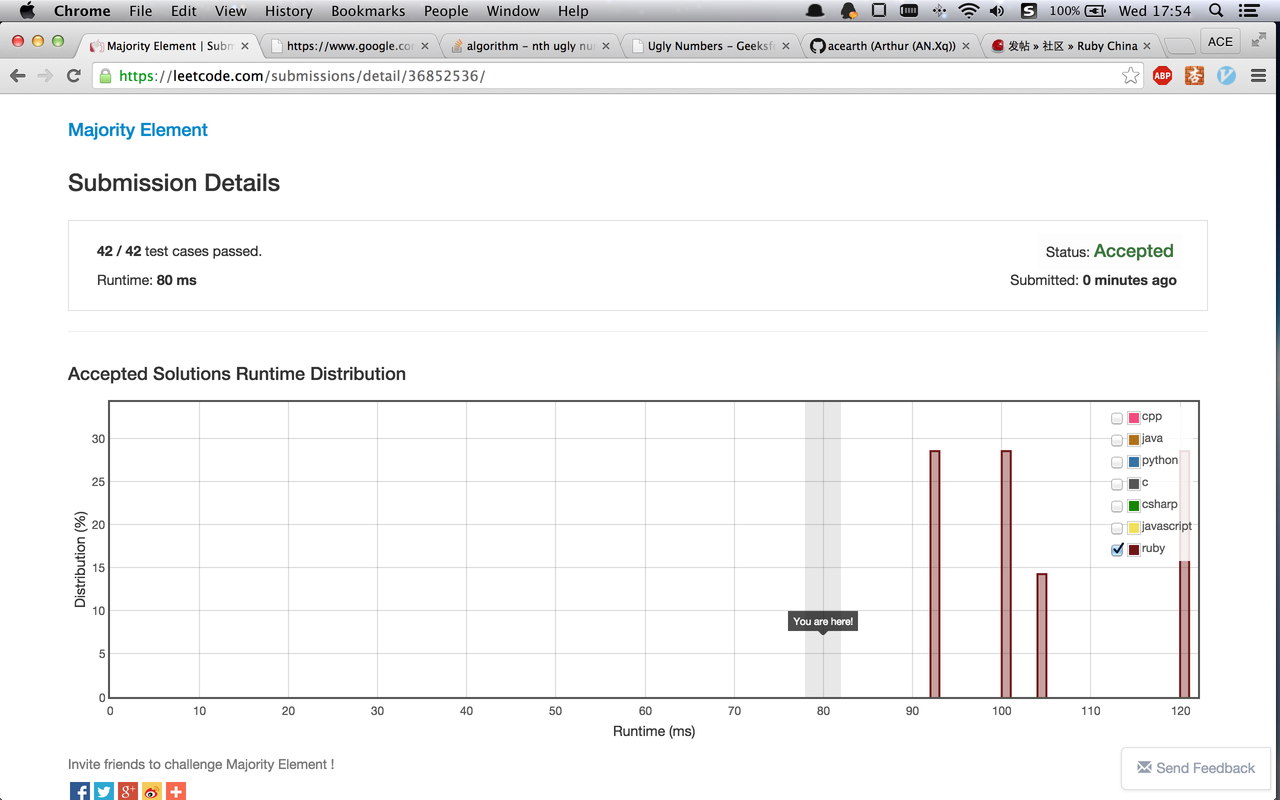
运行时间排名十分不稳定，这可能与目前 ruby 的提交量太少有关，但也与服务器有关。我的猜测是，如果有相邻两个时间分布式相同的，那得到这两种分布的概率是相同的。比如下图，92ms 和 104ms 的运行时间有相同的分布。如果这次运行时间是 92ms，下次也可能是 104ms。

做题训练很有价值这两百道题，至少有 170 道题目是自己想出来然后一行行 coding 提交 AC 的。现在回顾前面一百题，已经感觉自己原先的方法十分拙劣了。这算是做题的一个收获。

3.两道有趣的题目 3.1 majority elements 求一个元素中出现次数最多的元素。这个题目的常规解法是使用优化后的动态规划。遍历一遍数组得到结果。但一个更有效的方法是排序。先上代码

def majority_element(nums)
    nums.sort[nums.size/2]
end

其实上面的分布图就是该题使用排序法得到的结果，该法的运行时间明显优于其他方法。但是排序时间复杂度为 O(nlogn)，为何这里特别快？记得库函数中的 sort 方法都是三路快排加插入排序。在该题中，由于至少有一般的元素是相同的，所以插入的过程应该是直接插入尾部，这样时间几乎接近线性。但和传统方法比又少了若干次比较，所以更快。该法思路来源于同组同学。

3.2 find first missing one. 找出一个乱序数组中缺少的第一个正数。如 [4, 0 ,3,1] 缺少的第一个正数是 2。这题一般的思路是直接将正数值放入其对应下标，然后按序遍历数组，找到和值不对应的下标即为所缺。但这样仍然需要多次比较和读写数组（尽管是线性复杂度）。本人的思路如代码所示：

def first_missing_positive(nums)
  oldBase, base=0,0
  arr=[nums,nums.reverse]
  i=0
  loop do
    arr[i].each { |e| base=e if e==base+1 }
    break if base==oldBase
    oldBase,i=base,1-i
  end
  return base+1
end

首先记录当前已有的值（初始为零），然后按序遍历数组，如果 1 出现了，就找 2，2 出现了就找 3，直到找到为止。为了加速移动，并应对数组已经有序的情况，在正序遍历数组后再逆序遍历数组。和常规方法相比，该法的复杂度是 O(n*n)。但只要输入序列不是锯齿状（如快排的 killer adversary, 又如 [2,4,1,3]），该法在除锯齿状数据的情况以外运行时间都很短。在随机产生数据的前提下，我对两种思路的数据都做了实验，O(n*n) 的解法要快于 O(n) 法。但如果数据是用 knuth shuffle 洗牌的思路生成随机数组（如 [4,2,1,3]），只是将原组做了交换，缺失值为最大值的情况下，该法将产生很多循环，运行效果变差（在对 10000 个连续值 shuffle 后的数组处理）。用这种思路解题，运行时间 76ms，和其他方法的最优时间相同。

最后感谢关注了 leetcodePractice 的各位朋友，是你们带给我更大动力。特别感谢@quakewang，对我提出了许多批评的同时展示了许多书写良好的代码。本人 LeetcodePractice 项目地址：https://github.com/acearth/LeetCodePractice
欢迎批评和关注！

2 个赞

luikore #1 2015年08月19日

变量名用 snake case 更好些...

1 个赞

shy07 #2 2015年08月19日

下班前刚好刷到了 majority_element 这题，解法一模一样，我管它叫 fast and simple and cheat 另外贴一下三分之一那个问题的解法，正巧是从 @luikore 那里学到的：

def majority_element(nums)
  nums.sort.chunk{|x|x}.map(&:last).inject([]){|m,v| m << v[0] if v.size > nums.size / 3;m}
end

1 个赞

luikore #3 2015年08月19日

3.2 这样比较简单

def first_missing_positive(nums)
  b = Array.new nums.size + 1
  b[0] = true
  nums.each do |n|
    b[n] = true if n > 0
  end
  b.index nil or b.size
end

循环体内尽量少做运算就可以

1 个赞

luikore #4 2015年08月19日

其实 Ruby 的 bignum 实现用到的一个 bitset 的函数 nlz 可以调用 GCC 的 __builtin_clz, 而 __builtin_clz 会转换成处理器的 bsr/clz 指令，用 bitset 做这个运算，就可以少用很多内存，降低程序的 memory bandwidth. 而且 128 bit 的 clz 指令可以把第二次遍历的最后一次运算降低到 1/128

不过 bignum 并没有暴露 "set nth bit" 的 interface... 就做不到 C 的程度了

bitset + __builtin_clz:

#include <stdlib.h>
#include <memory.h>

typedef unsigned long l;
int firstMissingPositive(int* nums, int numsSize) {
    if (!numsSize) {
      return 1;
    }

    int llen = ((numsSize + sizeof(l) - 1) / sizeof(l));
    int lbits = sizeof(l) * 8;
    l* arr = malloc((llen + 1) * sizeof(l));

    // unset first bit
    memset(arr, 0xFF, (llen + 1) * sizeof(l));
    arr[0] &= ~(1UL << (lbits - 1));

    for (int i = 0; i < numsSize; i++) {
        if (nums[i] > 0) {
          int j = nums[i] / lbits;
          int k = nums[i] % lbits;
          arr[j] &= ~(1UL << ((lbits - 1) - k));
        }
    }

    int res = 0;
    for (int i = 0; i < llen; i++) {
      if (arr[i]) {
        res += __builtin_clzl(arr[i]);
        break;
      } else {
        res += lbits;
      }
    }
    free(arr);
    return res;
}

1 个赞

kewin #5 2015年08月20日

lz 还是 10.8 的系统？

arth #6 2015年08月20日

#1 楼 @luikore 恩，刚开始时还习惯用 java 的路数。。

arth #7 2015年08月20日

#5 楼 @kewin 10.9.

arth #8 2015年08月22日

#3 楼 @luikore 恩，这种使用 O(n) 空间的做法会让代码非常简洁。我用过循环赋值的方法，那样代码要累赘一点，但只用 O(1) 空间。各有优缺。

arth #9 2015年08月22日

#4 楼 @luikore 跑了一下，C 下 0ms

msg7086 #10 2015年08月23日

3.1 的正常解

def majority_element(nums)
    cnt = 0
    num = nums.first
    nums.each do |n|
        next cnt += 1 if n == num
        cnt -= 1
        cnt, num = 1, n if cnt < 0
    end
    num
end

拿了 88ms，好像并不算太慢。如果输入数据量很大的话排序可能会比遍历慢。

msg7086 #11 2015年08月23日

3.2 的 2B 解

def first_missing_positive(nums)
    tail = {}
    nums.each do |v|
        next if v <= 0
        next if tail[v]
        tail[v] = v
        if tail[v-1]
            tail[v] = tail[v-1]
            tail[tail[v]] = v
        end
        if tail[v+1]
            last = tail[v+1]
            tail[last] = tail[v]
            tail[tail[v]] = last
        end
    end
    tail[1] ? tail[1]+1 : 1
end

拿了 80ms

arth #12 2015年08月23日

#10 楼 @msg7086 代码很清爽

arth #13 2015年08月23日

#11 楼 @msg7086 这段代码看起来有些乱。。。

msg7086 #14 2015年08月24日

#13 楼 @arth 这个 2b 解法是直接从 Longest Consecutive Sequence 那边搬过来的，在 Hash 里把连续数字头尾相连成为片段。只不过原题是找最长片段，这里只要看从 1 开始的片段就行了。

killernova #15 2015年08月27日

➜  ~  PRY
[1] pry(main)> def majority_element(nums)
[1] pry(main)*   cnt = 0
[1] pry(main)*   num = nums.first
[1] pry(main)*   nums.each do |n|
[1] pry(main)*     next cnt += 1 if n == num
[1] pry(main)*     cnt -= 1
[1] pry(main)*     cnt, num = 1, n if cnt < 0
[1] pry(main)*   end
[1] pry(main)*   num
[1] pry(main)* end
=> nil
[2] pry(main)> a=[1,2,1,1,1,1,2,3,2,3,2,3,2,3,2,3,3,3]
=> [1, 2, 1, 1, 1, 1, 2, 3, 2, 3, 2, 3, 2, 3, 2, 3, 3, 3]
[3] pry(main)> majority_element a
=> 3
[4] pry(main)> a = [1,5,7,3,4,2,3,4,2,2,2,1,2,6,4,3,2,1,7,5,6,4,2,1,1]
=> [1, 5, 7, 3, 4, 2, 3, 4, 2, 2, 2, 1, 2, 6, 4, 3, 2, 1, 7, 5, 6, 4, 2, 1, 1]
[5] pry(main)> majority_element a
=> 1
[6] pry(main)>

@msg7086 请问第二个数组是什么情况？

msg7086 #16 2015年08月28日

#15 楼 @killernova

You may assume that the array is non-empty and the majority element always exist in the array.

torubylist #17 2016年01月13日

#3 楼 @luikore 大神。膜拜。＃3 的解法佩服地五体投地。

需要登录后方可回复, 如果你还没有账号请注册新账号

2 个赞

共收到 17 条回复

收到新回复，点击立即加载