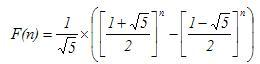第一个是 打印 斐波那契数,像 0 1 1 2 3 5 8 13 21 这样的
第二个 是找零算法
假设要用 50、20、10、5、1(元)找出 87 元来 make_change(87, [50,20,10,5,1)
#斐波那契数
#直接用递推,把之前的结果放在数组里面
def fibonacci step
arr = [0,1]
result = if step.to_i == 1
0
elsif step.to_i == 2
arr
else
temp = step.to_i - 2
temp.times do |i|
size = arr.size
arr << arr[size - 1] + arr[size - 2]
end
arr
end
puts result
end
第二个确实麻烦, 我的思路是从最大额的零钱开始,需要多少张, 再取余重复以上过程 (这个应该先排除上一个匹配的零钱,重新获取范围,我的没有做) 代码捉急啊
这种算法明显不是最优解,看计算出的结果就是了
def make_change money, coins = [50,20,10,5,1]
result = if money == 0
[]
elsif coins.include? money
[money]
else
coins_count = []
valid_coins = coins.select{ |coin| coin < money } #小于
remainder = money
valid_coins.each do |coin|
num = remainder/coin
remainder = remainder % coin
next if num == 0 #余数小于当前的匹配值 进行下一论匹配
num.times{ coins_count << coin }
break if remainder == 0 || remainder < valid_coins.min #匹配完毕或者没有合适结果
end
end
coins_count
end
各位具体说下找零的想法吧
PS 睡了段时间,去面的, 不知哪根神经抽抽儿 把公交卡放在家里 揣了个鼠标装包里就奔去了 都没弄出来,就当马后跑了
假设每人39美分的零钱
这 39 美分是干什么用的啊
~/sandbox ruby change.rb
50
20
10
5
1
1
这还不是最优解,怎么才是最优解啊
好简单的题目,第一个,递归 recursion,当然应该用 dynamic programming,就是把已经计算过的数据计算出来,当然也可以使用迭代来实现。第二个,greedy algorithm 的一般案例了
def fib(step, initial = [0, 1], results = [0])
i, j = initial
return fib(step-=1, [j , i + j ], results << j) if step > 0
results
end
fib(10)
# => [0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55]
def make_change(money, coins = [50,20,10,5,1], results = [])
change = coins.find { |i| money - i >= 0 }
left = money - change
results << change
return make_change(left, coins, results) if left > 0
results
end
第二题...
def make_change r, coins = [50,20,10,5,1]
coins.map do |c|
q, r = r.divmod c
q
end
end
edit
其实这道题应该是给些奇怪的 coin 配置,考 DP (动态规划) 的 但对于一般货币 (1,2,5,10,20,50,...) 这么整也能得到最优解... 原因见 #33 楼
@luikore 二题优解,我来个第一题。
def p_fib(len)
(0..len).map { |pos| (f = ->(x) { x < 2 ? x : f[x-1] + f[x-2] })[pos] }
end
我也来贴个结果
17l @recurlamlisp 的迭代方式 最优雅肯定妥妥的 但是效率惨不忍睹...
 35 个数字就要跑 11 秒 而且全部是 CPU 100%
我自己用了个笨办法 用数组递归 跟 6l @hysios 的思路类似 虽然不优雅 但是效率很快 500 个数字
35 个数字就要跑 11 秒 而且全部是 CPU 100%
我自己用了个笨办法 用数组递归 跟 6l @hysios 的思路类似 虽然不优雅 但是效率很快 500 个数字
a = [];(0..500).each{|i| r= (i<2 ? i : (a[-1]+a[-2]));a.push(r)};a
 不知道各位喜欢代码优雅的 还是效率更快的...
不知道各位喜欢代码优雅的 还是效率更快的...
如果面额是 [50,30,1] 需要找 60 块?所以说面额的设置是很有讲究的。Coursera 上有个相应的课程挺不错的 https://class.coursera.org/optimization-001/class/index
第二题参见 http://quake.iteye.com/blog/175886 。这个题目是有优化条件的,要求返回的零钱数尽可能少。否则有 1 分的话,直接写个循环给 39 或者 87 个就 ok 了。
只从第一个开始减不一定会得到最优解。
比如 make_change(14, [10, 7, 1]) ,的最优解是 [7, 7] ,只用 2 个单位。如果粗陋地从最大数开始,就会得出需要 1 个 10 和 4 个 1 的结果,那就是要用 5 个单位了。
虽然不是 ruby, 但是第一个我觉得可以贴一下文档里的例子..
import scala.math.BigInt
lazy val fibs: Stream[BigInt] = BigInt(0) #:: BigInt(1) #:: fibs.zip(fibs.tail).map { n => n._1 + n._2 }
fibs.take(1000).toList // 前1000个
@zj0713001 要效率那个那么写哦,玩 ruby 语法糖和 lambda 去了,完全只图好看哈!下面来个效率的
def fib(len)
arr, a, b = [], 0, 1
len.times do
arr << a
a,b = b, a+b
end
arr
end
@zj0713001 再来个经济适用型男的,嘿嘿
fib = Hash.new do |f, n|
f[n] = if n <= -2
(-1)**(n+1) * f[n.abs]
elsif n <= 1
n.abs
else
f[n-1] + f[n-2]
end
end
这里还有个适用男,哈哈
def fib
phi = (1 + Math.sqrt(5)) / 2
((phi**self - (-1 / phi)**self) / Math.sqrt(5)).to_i
end
还有个我喜欢的
def fib
a, b = 1, 1
lambda {ret, a, b = a, b, a+b; ret}
end
fib_gen = fib
10.times { p fib_gen.call }
=> 1
=> 1
=> 2
=> 3
=> 5
=> 8
=> 13
=> 21
必须 Prolog 啊,输入一遍题目就可以了
#!/usr/bin/swipl -q -g main -f
:- use_module(library(simplex)).
coins -->
constraint(integral(c(50))),
constraint(integral(c(20))),
constraint(integral(c(10))),
constraint(integral(c(5))),
constraint(integral(c(1))),
constraint([c(50)] >= 0),
constraint([c(20)] >= 0),
constraint([c(10)] >= 0),
constraint([c(5)] >= 0),
constraint([c(1)] >= 0),
constraint([50*c(50), 20*c(20), 10*c(10), 5*c(5), 1*c(1)] = 87),
minimize([c(50), c(20), c(10), c(5), c(1)]).
main :-
gen_state(S0),
coins(S0, S),
variable_value(S, c(50), C50),
variable_value(S, c(20), C20),
variable_value(S, c(10), C10),
variable_value(S, c(5), C5),
variable_value(S, c(1), C1),
io:format("~w*50 ~w*20 ~w*10 ~w*5 ~w*1~n", [C50, C20, C10, C5, C1]),
halt.
Prolog 无压力
#!/usr/bin/swipl -q -g main -f
:- use_module(library(simplex)).
coins -->
constraint(integral(c(50))),
constraint(integral(c(30))),
constraint(integral(c(1))),
constraint([c(50)] >= 0),
constraint([c(30)] >= 0),
constraint([c(1)] >= 0),
constraint([50*c(50), 30*c(30), 1*c(1)] = 60),
minimize([c(50), c(30), c(1)]).
main :-
gen_state(S0),
coins(S0, S),
variable_value(S, c(50), C50),
variable_value(S, c(30), C30),
variable_value(S, c(1), C1),
io:format("~w*50 ~w*30 ~w*1~n", [C50, C30, C1]),
halt.
Prolog
#!/usr/bin/swipl -q -g main -f
:- use_module(library(simplex)).
coins -->
constraint(integral(c(10))),
constraint(integral(c(7))),
constraint(integral(c(1))),
constraint([c(10)] >= 0),
constraint([c(7)] >= 0),
constraint([c(1)] >= 0),
constraint([10*c(10), 7*c(7), 1*c(1)] = 14),
minimize([c(10), c(7), c(1)]).
main :-
gen_state(S0),
coins(S0, S),
variable_value(S, c(10), C10),
variable_value(S, c(7), C7),
variable_value(S, c(1), C1),
io:format("~w*10 ~w*7 ~w*1~n", [C10, C7, C1]),
halt.
#!/usr/bin/swipl -q -g main -f
:- use_module(library(simplex)).
coins -->
constraint(integral(c(100))),
constraint(integral(c(50))),
constraint(integral(c(20))),
constraint(integral(c(5))),
constraint([c(100)] >= 0),
constraint([c(50)] >= 0),
constraint([c(20)] >= 0),
constraint([c(5)] >= 0),
constraint([c(100)] =< 1),
constraint([c(50)] =< 1),
constraint([c(20)] =< 3),
constraint([c(5)] =< 1),
constraint([100*c(100), 50*c(50), 20*c(20), 5*c(5)] = 160),
minimize([c(100), c(50), c(20), c(5)]).
main :-
gen_state(S0),
coins(S0, S),
variable_value(S, c(100), C100),
variable_value(S, c(50), C50),
variable_value(S, c(20), C20),
variable_value(S, c(5), C5),
io:format("~w*100 ~w*50 ~w*20 ~w*5~n", [C100, C50, C20, C5]),
halt.
是的... 不过对一般货币如现在的人民币/美元的面额配置是最优解:
如果一个解法是最优解, 那其中除了最大面额外,1,5,10,50,100,500,...等面额都最多是 1 张 (如果有 2 张,可以抽出来替换成 x2 的面额). 而其中 2,20,200,...等面额最多是 2 张 (如果有 3 张 2,可以抽出来替换成 1 张 5 和 1 张 1). 所以最优解里,每一十进位上的和最多是 1+2*2+5 = 10, 但 = 10 就能替换成 1 张 10, 不算最优解了,所以和最多是 9. 于是最优解里小面额的总和不超过 999... , 还是小于 1 张最大面额. 综上,对于人民币/美元,粗鄙解得出来的结果和最优解一致。
@gihnius 粗鄙改造 luikore 的解法,不一定是最优结果,但是满足要求。
def make_change r, coins = {50 =>1, 20=>2, 10=>3, 5=>4, 1=>5}, result=[]
coins.each do |c, amount|
try = r.divmod(c)
if try.first <= amount
coins.delete(c)
result << try.first
result << make_change(try.last, coins)
else
r = r-c*amount
coins.delete(c)
result << amount
result << make_change(r, coins)
end
end
result.flatten
end
@bhuztez Prolog 是挺好玩的,再来一个解法总数的例子。我来个 ruby 的:
def make_change2(amount, coins)
n, m = amount, coins.size
table = Array.new(n+1){|i| Array.new(m, i.zero? ? 1 : nil)}
for i in 1..n
for j in 0...m
table[i][j] = (i<coins[j] ? 0 : table[i-coins[j]][j]) +
(j<1 ? 0 : table[i][j-1])
end
end
table[-1][-1]
end
#!/usr/bin/swipl -q -g main -f
:- use_module(library(clpfd)).
:- use_module(library(aggregate)).
coins([C50, C20, C10, C5, C1]) :-
Vars = [C50, C20, C10, C5, C1],
Vars ins 0 .. sup,
50*C50 + 20*C20 + 10*C10 + 5*C5 + C1 #= 87,
labeling([], Vars).
main :-
aggregate_all(count, coins(_), Count),
io:format("~w~n", [Count]),
halt.
#30 楼 @bhuztez 这是开挂啊。看了下 Ruby 下也有些现成的 CP solver 的封装,比如这个 http://gecoder.rubyforge.org/documentation/index.html
@luikore @bhuztez @doitian 玩 Constraint 这种 Logic,用不好玩了,写个或者扩展个才 hacking. 看这里,看这里,http://minikanren.org/
我也玩一个简单的,DP 算法:找零钱需要最小零钱数量。
def make_change(par, changes)
change_used = []
change_used[0] = 0
1.upto(par) do |cur| #从1块钱开始算
min_change = cur
changes.each do|value|
if value <= cur
temp = change_used[cur - value] + 1 #已知的动态规划找零问题递推式
min_change = temp if temp < min_change
end
end
change_used[cur] = min_change
puts "找#{cur}块零钱最少需要#{min_change}张零钱"
end
end
make_change(87, [50, 20, 10, 5, 1])
看来 LZ 挺喜欢用 result = if ... 这类结构的。看大神们写的方法要琢磨好久。。真是智捉。我还是用最基本方法好了。
def fib(n)
return n if n <= 1
fib(n-1) + fib(n-2)
end
(0...9).each { |n| p fib(n).to_s+' ' }
make_change(87, [50, 20, 10, 5, 1]) => [1, 1, 1, 1, 2] 是 50*1 +20*1+10*1+5*1+1*2 = 87 差了点东西
def make_change(money, coins)
dp = [0]
path = []
result = {}
coins.each_with_index do |coin, index|
coin.upto(money) do |i|
if !dp[i - coin].nil? && (dp[i].nil? || dp[i - coin] + 1 < dp[i])
dp[i] = dp[i - coin] + 1
coins[index] += 1
path[i] = i - coin
end
end
end
if path[money].nil?
puts "impossible." and return
end
i = money
loop do
break if path[i].nil?
result[i - path[i]] ||= 0
result[i - path[i]] += 1
i = path[i]
end
p result # 具体解
puts dp[money] # 硬币数
end
这个和 @blackanger 的算法相同,多了记录具体解
#56 楼 @nickelchen @blackanger 这个递归看上去比较好,但实际上复杂度是O(2^n)的。
@shooter 的斐波那契的复杂度是 O(n) 的
实际上用矩阵乘法,复杂度是可以到 O(logn) 的
如下
require 'matrix'
def fab(n)
return 0 if n == 0
m = Matrix[[1, 1], [1, 0]]
mul([m] * n)[0, 1]
end
def mul(matrices)
return matrices[0] if matrices.size == 1
mid = matrices.size / 2
return mul(matrices[0, mid]) * mul(matrices[mid..-1])
end
(1..10).each { |n| puts fab(n) }
# 1
# 1
# 2
# 3
# 5
# 8
# 13
# 21
# 34
# 55
def count_with_record(money,money_kinds,used,way = [],ways)
if money == 0
ways << way
return 1
elsif money < 0 or money_kinds.empty?
return 0
end
way1 = copy(way)
way1 << money_kinds[0]
way2 = way
return count_with_record(money - money_kinds[0],money_kinds,money_kinds[0],way1,ways) + count_with_record(money,money_kinds[1..-1],0,way2,ways)
end
def copy(arr)
r = []
arr.each do |e|
r << e
end
return r
end
money_kinds = [3,2,1]
money = 5
ways = []
way = []
puts count_with_record(money,money_kinds,way,ways)
puts "should be 5"
puts "all the combination"
puts ways.inspect
写的丑了些。。。
fib,可以一边递归,一遍记录(放到 hash 里面),这样复杂度应该可以。
@blackanger @xranthoar 前面人用了 Greedy approach 解,后面大家又用 Dynamic Programming . 我也在来个 dp,Greedy approach 太短了确实精简了,还是挺喜欢 Greedy approach
def make_change(amount, coins = [25, 10, 5, 1])
coins.sort! { |a, b| b <=> a }
optimal_change = Hash.new do |hash, key|
hash[key] = if key < coins.min
[]
elsif coins.include?(key)
[key]
else
coins.
reject { |coin| coin > key }.
inject([]) {|mem, var| mem.any? {|c| c%var == 0} ? mem : mem+[var]}.
map { |coin| [coin] + hash[key - coin] }.
reject { |change| change.inject(&:+) != key }.
min { |a, b| a.size <=> b.size } || []
end
puts hash
hash[key]
end
optimal_change[amount]
end
#68 楼 @blacktulip fib 通项公式同样是 O(logn), 计算比矩阵法多...
浮点求幂也有 O(1) 的实现,方法是利用 x86 上的两个浮点指令 FYL2X (求 2 为底的对数), F2XM1 (求 2 为底的幂), 把 x**n 转换成 2 ** (n * log2(x)), 每步操作都是常数级,那就 O(1) 了... 但实际上这两个指令耗费大量的时钟周期,比求整数次幂的 O(logn) 算法慢...
第一题这么做可以么?
def f t
a, b = 0, 1
t.times do
print a, " "
a, b = b, a + b
end
end
f 200
第二题就这么干吧
def make_carge money
choice = [50, 20, 10, 5, 1]
result = [0, 0, 0, 0, 0]
point = 0
while money != 0
if(money >= choice[point])
money -= choice[point]
result[point] += 1
else
point += 1
end
end
5.times do |i|
print choice[i], ' : ', result[i], "\n"
end
end
make_carge 87
或者干掉一个数组
def make_carge money
choice = [50, 20, 10, 5, 1]
result = 0
point = 0
while money != 0
if(money >= choice[point])
money -= choice[point]
result += 1
else
point += 1
print result, " "
result = 0
end
end
puts result
end
make_carge 4201
@xranthoar @sqrh @luikore @blacktulip 算法效率确实都是 O(log(n)), 不错!
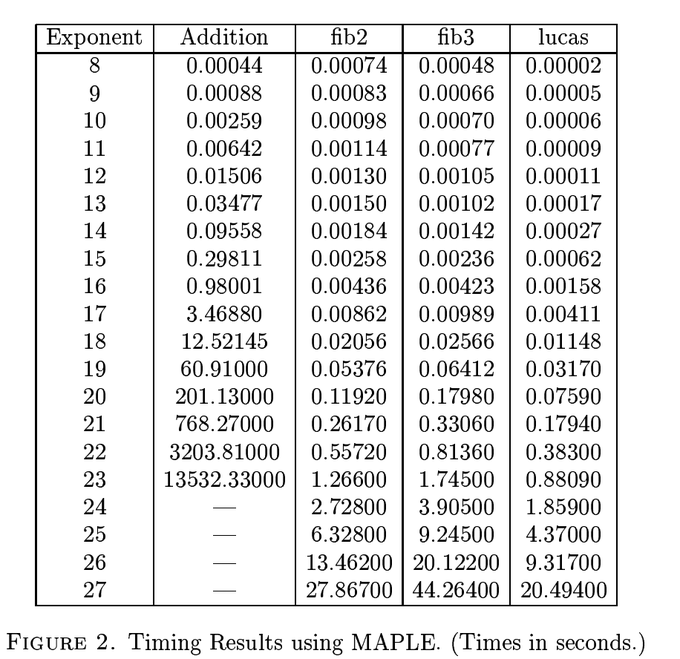
这个两个算法应该都是对大数据计算来说的吧,浮点计算不精确这个说法应该就忽略了吧。而且,在现代计算机的浮点计算不是 x86 的两条指令 FYL2X 和 F2XM1 可以概括的吧!从下面这个结果可以看出,我们的 Two-Term CRT 和 The Lucas Numbers 在现在的计算机的表现是相近的吧(虽然这个结果 The Lucas Numbers 更胜一筹),就是不知道更多的大型机上的那个表现更加的完美。
#32 楼 @bhuztez prolog 看上去的确很牛啊,这几天开始看 prolog 了。ruby 真不方便干这些事,这是我的 ruby 方案,有点费劲:
def make_changes(need, coins, feed = {})
valid_coins = coins.keys.select{|c| c <= need && coins[c] > 0 }.sort.reverse
valid_coins.each do |c|
feed[c] ||= 0
feed[c] += 1
return feed if c == need
coins[c] -= 1
f = make_changes( need - c, coins, feed)
return f if f
end
end
#> make_changes 160, { 1 => 4, 5 => 1, 10 => 1, 50 => 1, 100 => 1}
=> {100=>1, 50=>1, 10=>1}
#> make_changes 160, { 1 => 4,5 => 2, 10 => 0, 50 => 1, 100 => 1}
=> {100=>1, 50=>1, 5=>2}
关于第一题:
def fibonacci(n, cache=Hash[[[0,0],[1,1]]])
return cache[n] if cache[n]
cache[n] = fibonacci(n-2, cache) + fibonacci(n-1, cache)
end
puts (1...1000).to_a.collect{|t| fibonacci(t) }.join(', ')
斐波那契函数的经典解决方案是使用递归 (太精深的数学实在不懂,比如 26 楼的方案), 常规的方法在小数字上很容易,但一旦数字过大,计算量就相当恐怖,这里用了个缓存 Hash, 即使数字达到 1000, 基本上一运行就能得出结论。
斐波那契数 arr = [0, 1] step = 8 (1..step).each {|i| arr << arr[-2] + arr[-1]} ==> [0, 1, 1, 2, 3, 5, 8, 13, 21, 34]