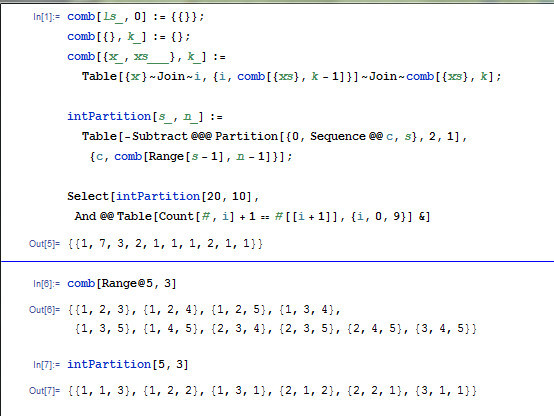
0 在这十句话里出现的次数是 (); 1 在这十句话里出现的次数是 (); 2 在这十句话里出现的次数是 (); 3 在这十句话里出现的次数是 (); 4 在这十句话里出现的次数是 (); 5 在这十句话里出现的次数是 (); 6 在这十句话里出现的次数是 (); 7 在这十句话里出现的次数是 (); 8 在这十句话里出现的次数是 (); 9 在这十句话里出现的次数是 ()。 要求括号里所填的答案是数字 (0-9). 哪位大神能用 ruby 写个脚本能算出结果来,答案是 1,7,3,2,1,1,1,2,1,1
每个数字至少出现 1 次,一共 20 个数字,所以填的数字的和是 20, 有了这两个条件,就好办了:
def check seq
0.upto 9 do |i|
return false if seq.count(i) + 1 != seq[i]
end
true
end
def calc seq, rest_sum
if seq.size == 10
p seq if rest_sum == 0 and check seq
else
1.upto 9 do |i|
break if rest_sum < i
calc seq + [i], rest_sum - i
end
end
end
calc [], 20
#5 楼 @bhuztez 去掉这个要求是可以的... 不过总次数变成最多 20, 去掉这个要求而修改的程序如下
def calc seq, rest_sum
if seq.size == 10
p seq if rest_sum == seq.count{|i|i>9} and (0..9).all?{|i| seq.count(i) + 1 == seq[i]}
else
1.upto 10 do |i|
break if rest_sum < i
calc seq + [i], rest_sum - i
end
end
end
calc [], 20
$ ruby sum.rb
[1, 7, 3, 2, 1, 1, 1, 2, 1, 1]
[1, 10, 1, 1, 1, 1, 1, 1, 1, 1]
@luikore 如果去掉 0-9 这个要求 次数为 20 是不成立的,因为 10 是能看成 1 和 0 的,这样的话这道题目用代码写会更难一点,要涉及字符了
还是 Prolog 了
:- use_module(library(clpfd)).
count([], _, 1).
count([H|T], N, C) :-
N #= H,
C #= C1 + 1,
count(T, N, C1).
count([H|T], N, C) :-
N #\= H,
count(T, N, C).
problem(Solution) :-
Solution = [C0, C1, C2, C3, C4, C5, C6, C7, C8, C9],
Solution ins 0..9,
count(Solution, 0, C0),
count(Solution, 1, C1),
count(Solution, 2, C2),
count(Solution, 3, C3),
count(Solution, 4, C4),
count(Solution, 5, C5),
count(Solution, 6, C6),
count(Solution, 7, C7),
count(Solution, 8, C8),
count(Solution, 9, C9).
prolog 这样的东西会让人思维退化,下面的代码对所有 n>6 工作,对于 n<=6, 暴力搜索。复杂度是 O(n)(或者说 O(1))
def calc n
([1] * n).tap do |ret|
ret[1] = n-3
ret[2] = 3
ret[3] = 2
ret[n-3] = 2
end
end
import random
seq = [random.randint(0, 9) for i in range(10)]
while True:
seq1 = []
for i in range(10):
seq1.append(seq.count(i)+1)
if seq == seq1:
print seq
break
seq = seq1
用迭代的话,除了输出答案,还有就是在 [1, 8, 2, 1, 2, 1, 1, 2, 1, 1] 和 [1, 7, 4, 1, 1, 1, 1, 1, 2, 1] 循环,不知道怎样解决这个问题
#21 楼 @YangZX 别怕,黑脸没啥,大家就事论事讨论呗。 昨天和 @luikore 了解这方面的概念,发现有一个重点是我一开始没搞清的——constraint 本身是无序的,而真实执行的时候,计算机就有机会找到各种”短路条件“进行优化,科学家们要做的,就是找到那些短路方法,并用抽象工具将其普遍化。所以,constraint programming 最大的优势是你不会对计算机进行瞎指挥,也就是给了它最大限度的优化空间,这个道理和声明式编程的优势一样。
对这句话吐个嘈:
即使是最好的prolog编译器,实现的自动搜索比得上你自己去发掘出的剪枝或者说其他更高效的算法有效吗
N 年前,有人鄙视 java 的 GC,也说过类似的话——”机器的 GC 能比的上我自己回收的效果好吗?“ 再 N 年前,有人鄙视编译器,也说过类似的话——“编译器的优化,比得上我自己直接写汇编指令吗?”
当我第一次用 prolog 尝试写个 sudoku solver 的时候我就对 prolog 深表失望了,
其实还好吧,简单的不到一秒就能解出来的 ... 太难的,人脑就更解不出了。
1..你看楼上那个 prolog 代码,完全是充满了重复,完全可以用一个循环来表示那些逻辑嘛
我想写得土一点 ... 对于一个不熟悉 Prolog 的人来说这样容易猜出代码啥意思,反正就这么几行...
即使是最好的 prolog 编译器,实现的自动搜索比得上你自己去发掘出的剪枝或者说其他更高效的算法有效吗?
不能啊,Prolog 可是通用的,必须比不过专门的算法 ...
Prolog 就特别适合解这类脑残的题 ...
但 Java 的 GC 强大也没用啊
Java 的 JIT 虽然很强大,代码运行速度很快,而且不像 Erlang 整天 Copy 来 Copy 去的,但是等 GC 开始搬数据了,真的是要什么都没有了
而且,很多写 Java 的好像都没内存池的概念的?相关的数据一定要尽量放在一起,不然内存碎片就足够坑死你了。
#22 楼 @fsword #23 楼 @bhuztez 其实我对 prolog 不是很了解,我胡乱吐槽所以感觉压力很大。。 不过最初我在看 SICP 的时候,在第四章看到了一个和 prolog 很像的基于逻辑的数据库,立马就被吓尿了,的确是一行代码就没写就做了很多事情啊。。。 总的来说我对 prolog 的看法是:
- prolog 的确是很有用的工具,让人能够专注于问题的逻辑,并且通过简单的代码就能实现高效的搜索
- prolog 的最大问题是,他屏蔽了你对问题的深入探讨的欲望。假设你满足于一个效率比较低,但能够勉强忍受的程序,你就不会想去得到一个更优的算法。
总的来说,如果我确定了一个问题是 NPC(或者 NPHard),我会毫不犹豫用 prolog
不过我尝试 prolog 写的数独的效率比我自己实现的差得太远太远了。。难道现在改进 prolog 的人不是这样做的?
sudoku,Prolog 肯定比不过 DLX 的,的确是差好远好远啊 ...
其实运行速度,还好吧,我用下面这样的代码算过,简单的题目也不慢啊
写成这副样子是为了让不会写代码的人自己搞定...
:- use_module(library(clpfd)).
sudoku(Puzzle, Solution) :-
Puzzle = Solution,
Puzzle = [
[ A1, A2, A3, A4, A5, A6, A7, A8, A9 ],
[ B1, B2, B3, B4, B5, B6, B7, B8, B9 ],
[ C1, C2, C3, C4, C5, C6, C7, C8, C9 ],
[ D1, D2, D3, D4, D5, D6, D7, D8, D9 ],
[ E1, E2, E3, E4, E5, E6, E7, E8, E9 ],
[ F1, F2, F3, F4, F5, F6, F7, F8, F9 ],
[ G1, G2, G3, G4, G5, G6, G7, G8, G9 ],
[ H1, H2, H3, H4, H5, H6, H7, H8, H9 ],
[ I1, I2, I3, I4, I5, I6, I7, I8, I9 ]
],
maplist(all_different,
[
[ A1, A2, A3, A4, A5, A6, A7, A8, A9 ],
[ B1, B2, B3, B4, B5, B6, B7, B8, B9 ],
[ C1, C2, C3, C4, C5, C6, C7, C8, C9 ],
[ D1, D2, D3, D4, D5, D6, D7, D8, D9 ],
[ E1, E2, E3, E4, E5, E6, E7, E8, E9 ],
[ F1, F2, F3, F4, F5, F6, F7, F8, F9 ],
[ G1, G2, G3, G4, G5, G6, G7, G8, G9 ],
[ H1, H2, H3, H4, H5, H6, H7, H8, H9 ],
[ I1, I2, I3, I4, I5, I6, I7, I8, I9 ],
[ A1, B1, C1, D1, E1, F1, G1, H1, I1 ],
[ A2, B2, C2, D2, E2, F2, G2, H2, I2 ],
[ A3, B3, C3, D3, E3, F3, G3, H3, I3 ],
[ A4, B4, C4, D4, E4, F4, G4, H4, I4 ],
[ A5, B5, C5, D5, E5, F5, G5, H5, I5 ],
[ A6, B6, C6, D6, E6, F6, G6, H6, I6 ],
[ A7, B7, C7, D7, E7, F7, G7, H7, I7 ],
[ A8, B8, C8, D8, E8, F8, G8, H8, I8 ],
[ A9, B9, C9, D9, E9, F9, G9, H9, I9 ],
[ A1, A2, A3, B1, B2, B3, C1, C2, C3 ],
[ A4, A5, A6, B4, B5, B6, C4, C5, C6 ],
[ A7, A8, A9, B7, B8, B9, C7, C8, C9 ],
[ D1, D2, D3, E1, E2, E3, F1, F2, F3 ],
[ D4, D5, D6, E4, E5, E6, F4, F5, F6 ],
[ D7, D8, D9, E7, E8, E9, F7, F8, F9 ],
[ G1, G2, G3, H1, H2, H3, I1, I2, I3 ],
[ G4, G5, G6, H4, H5, H6, I4, I5, I6 ],
[ G7, G8, G9, H7, H8, H9, I7, I8, I9 ]
]),
append(Puzzle, Rows),
Rows ins 1..9,
labeling([ff], Rows).
见到大牛了多多请教下
我不是什么大牛 ...
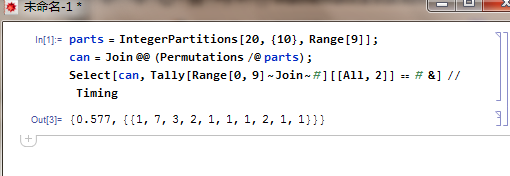 如果再增加一行代码,运行时间会小于 0.1s
如果再增加一行代码,运行时间会小于 0.1s