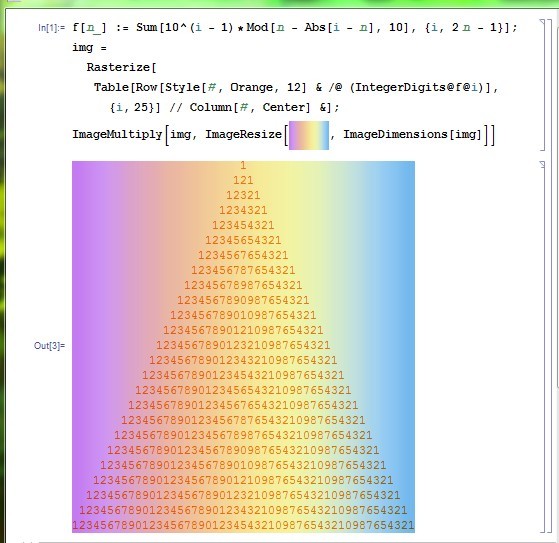
见别人用 Java 写的有数十行代码,想看看 ruby 程序员会如何来做。
我会这么写:
n = gets.to_i n.times do |i| print ' '*(n-1-i) 1.upto(i+1){|j| print j} i.downto(1){|j| print j} puts end
我不是 ruby 程序员,我还只是个初学者。
puts (1..n).inject('') { |str, i| str+' '*(n-i)+(1..i).to_a.join('')+(1..i-1).to_a.join('').reverse+"\n" }
一行代码,不过有点繁琐,等待更简洁的答案
def f(n)
(1...n).inject('') {|s, i| s << i.to_s }.tap {|i| i << i.reverse}.insert(n-1, n.to_s)
end
(1..9).each {|i| puts f(i).center(17)}
# 根据输入
gets.to_i.tap {|n| (1..n).each {|i| puts f(i).center(n*2 - 1)}}
zgm
#5
2012年09月22日
gets.to_i.tap{|n|(1..n).each{|m|puts " "*(n-m)+((1..m).to_a+(1..m-1).to_a.reverse).join}}
def pyramid(n)
1.upto(n) do |i|
puts ((1..i).to_a + (1...i).to_a.reverse).join.center(n * 2 - 1)
end
end
def pyramid(n)
prefix = []
1.upto(n) do |i|
puts [prefix, i, prefix.reverse].flatten.join.center( 2 * n - 1)
prefix.push(i)
end
end
def pyramid(n)
prefix = ''
1.upto(n) do |i|
puts (prefix + i.to_s + prefix.reverse).center(2 * n - 1)
prefix[i-1] = i.to_s
end
end
应该算是另一种思路的吧
chyanog
#15
2012年09月22日
chyanog
#20
2012年09月23日
#!/usr/local/bin/ruby
require 'mathn'
def f(n)
return -(20000000/9999999999)*1024**(-4/5-(1/10)*n).ceil*9765625**(-4/5-(1/10)*n).ceil*100**n-(50000/9999999999)*1024**(-1/2-(1/10)*n).ceil*9765625**(-1/2-(1/10)*n).ceil*100**n-(2000/3333333333)*1024**(-2/5-(1/10)*n).ceil*9765625**(-2/5-(1/10)*n).ceil*100**n-(80/9999999999)*1024**(-1/5-(1/10)*n).ceil*9765625**(-1/5-(1/10)*n).ceil*100**n+(80000000/9999999999)*1024**((1/10)*n+1/10).floor*9765625**((1/10)*n+1/10).floor+(200000/3333333333)*1024**((1/10)*n+3/10).floor*9765625**((1/10)*n+3/10).floor+(50000/9999999999)*1024**((1/10)*n+2/5).floor*9765625**((1/10)*n+2/5).floor+(4000/9999999999)*1024**((1/10)*n+1/2).floor*9765625**((1/10)*n+1/2).floor-(400000/9999999999)*1024**(-((1/10)*n+3/5).floor)*9765625**(-((1/10)*n+3/5).floor)*100**n+(20/9999999999)*1024**((1/10)*n+7/10).floor*9765625**((1/10)*n+7/10).floor-(1/1111111111)*100**n*10000000000**(-((1/10)*n+1/10).floor)+(7000000/9999999999)*10000000000**((1/10)*n+1/5).floor-(700/9999999999)*10000000000**(-((1/10)*n+3/10).floor)*100**n+(100/3333333333)*10000000000**((1/10)*n+3/5).floor-(1000000/3333333333)*10000000000**(-((1/10)*n+7/10).floor)*100**n+(1/9999999999)*10000000000**((1/10)*n+4/5).floor-(100000000/9999999999)*10000000000**(-((1/10)*n+9/10).floor)*100**n+(100000000/1111111111)*10000000000**((1/10)*n).floor+(13717421/1111111111)*100**n-109739369/1111111111`
end
n=20
1.upto(n){|i| puts f(i).to_s.center(2*n-1)}
经过不懈努力,通用的版本已经搞定,可以完美运行
lolychee
#24
2012年09月23日
#!/usr/bin/env ruby
gets.to_i.tap do |n|
(1..n).each {|i| puts ((a = (1...i).collect{|x| x%10 }.to_a.join) + (i%10).to_s + a.reverse).center(n*2-1) }
end
这是通用版 好难看的一坨
chyanog
#25
2012年09月23日
x=15
1.upto(x){|n| puts (1..2*n-1).map{|i| (n-(n-i).abs)%10 }.join.center(2*x-1) }
1.upto(x){|n| puts ( ((1..n).to_a+(n-1).downto(1).to_a).map{|i| i%10}).join.center(2*x-1) }
两种方法
mvj3
#26
2012年09月24日
翻出自己一年前的也是用平反算的版本 https://gist.github.com/1261488
(1..(ENV['NUM']||='42').to_i).each {|num| puts "#{' '*(ENV['NUM'].to_i - num)}#{('1'*num).to_i**2}" }
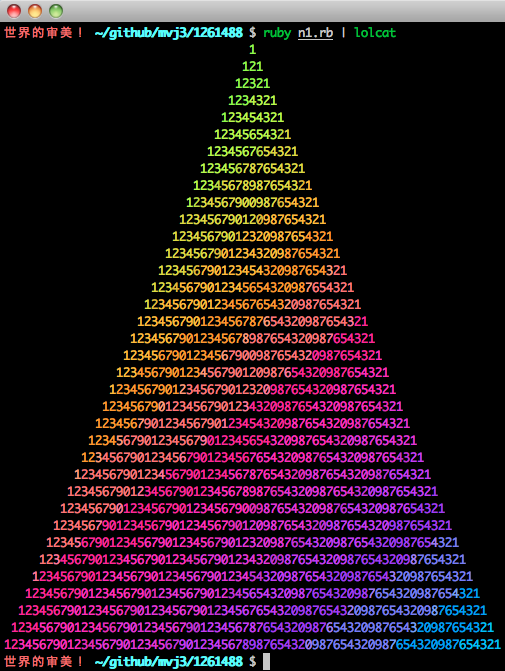
本质上就是两个规则: 1, 依次为 '1'*n 的平方 2, 按最长一列的中线居中。
String#center都几乎忘记了,比上面的罗嗦点
(1..(ENV['NUM']||='42').to_i).each {|num| puts (('1'*num).to_i**2).to_s.center(ENV['NUM'].to_i*2-1) }
mvj3
#32
2012年09月24日
#28 楼 @chyanog 哈哈,只当回复你 11 楼了~
不过按下面这位台湾人的思路来就对称了 www.khjh.kh.edu.tw/science40/初小/初小數學2/初小數學2.htm
1.我們終於明白為何書上最多介紹到九層,就是因為阿拉伯數碼最多到9而已。換言之,從第十層10個1的平方開始,每一層皆會發生進位效應,而使表象似乎不再有規律,同時也出現「0」數碼。因此假若每一個數目,都有其專門唯一數碼表示,而非由基本數碼組合而成,則ㄓ個1的平方積,一定為通式如下的結構:12345… … …(ㄓ-1)ㄓ(ㄓ-1) … … …54321,為一個(2ㄓ-1)奇位數的數目。
2.自第十層開始,原先簡單趣味不再,那麼是真的不再有規律,還是另有別種風味﹖我們仔細慢慢研究,終於有了發現:我們都知道數學裡有所謂循環小數、循環節的特性,沒想到這座塔竟然也有極其類似的「九位循環節」構造,可令人讚嘆不已!且讓我們慢慢說來:例如第十三層之結構
(1)設每一數目皆有專門數碼,則13個1的平方積為
123456789(10)(11)(12)(13)(12)(11)(10)987654321
(2)今因10以上,皆會進位,而由兩個基本數碼組合表示,所以其積組合後狀況為
123456789 987654321
10 10
11 11
1212
+ 13
1234567901234320987654321
因為進位效應,原有簡單規律不再,而「0」數碼出現,但仍為(2ㄓ-1)奇位數的數目。
chyanog
#33
2013年03月29日
发现 stack exchange 上面也有玩这个的,http://codegolf.stackexchange.com/questions/8696/print-this-diamond