之前写过一篇博客是关于 Linear Hash 的，但实际上没讲清楚，今天看了别人的讲法，这里做一个总结。

Background

我们知道，hash 需要先创建一个一定长度的数组，之后再通过 hash function 把 key 映射到这个数组里。

如果随着插入的数据增多，数组被填满后，需要将数组变大，这个过程称为 resize。

因为 resize 会改变数组的长度，所以在 resize 的时候需要加锁（或者说 latch）保证正确性，这个时候，不能读，也不能写。

也就是说会造成卡顿，这种情况对于高性能的存储结构是不可接受的（当然也有不处理的，比如 Rust 的 dashmap）。

Description

假设我们现在的数组 a 的长度是是 4。

这个时候数组满了，需要 resize。Extensible Hash 的做法是，把数组的长度加倍变成 8。

元素少的时候还好，多的话，就会有很长一段时间不能读写。

我们先来看直接加倍是什么情况。

我们需要把 a[0] 内的元素，重新分配给 a[0] 和 a[4]，a[1] -> a[1], a[5]，a[2] -> a[2], a[6]，a[3] -> a[3], a[7]。

如下图：

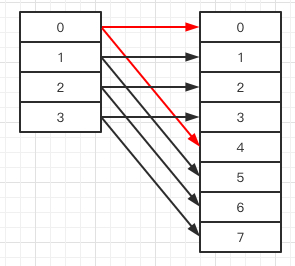
现在为了不想把每个元素 resize，我们只增加一个元素 a[4]。因为原来在 a[0] 的元素有两个位置，所以需要把 a[0] 的元素重新分配到 a[0] 和 a[4]。

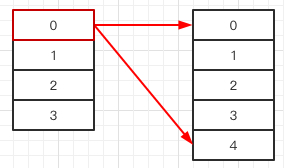
由于 a[1]、a[2]、a[3] 内的元素没有被重新分配。所以我们在查找元素的时候，需要能分辨，应该在 1 ~ 3 里找，还是 0 和 4 里找。

方法也很简单，还是用之前的 hash function，既 hash(key) % 4。

如果得到的值是 1、2、3 的话，我们知道，这个些元素还没有被 resize，所以需要在 a[1]、a[2]、a[3] 找。

如果是 0 的话，由于 a[0] 已经被 resize 了，有可能在 a[0] 或者 a[4] 里，这个时候我们只要模 8，既 hash(key) % 4 就可以得到具体的位置。

实现起来也很简单，只需要一个 cursor，指向下一个要被 resize 的 index 就可以。

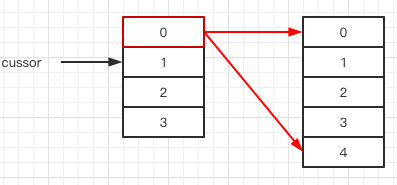
代码描述如下：

def index(key)
  i = hash(key) % @n

  if i < @curssor
    i = hash(key) % (@n * 2)
  end

  index
end

Summary

去年看 Linear Hash 的时候，先看的 Erlang ETS 的源码，没看懂。后来又找了一个课件，然后回过头有扒了一遍 ETS 的源码，着实费了一番功夫。。。

但今天看了 CMU 15-445 Lecture #06: Hash Tables，发现其实 20 分钟就可以搞明白。

想说的是，可能直接看源码有的时候不见得是明智之举。学习算法，相比实现细节，更重要的是搞清楚算法背后的思路。