算法从 LRU 到 LIRS

early · 2019年05月13日 · 最后由 early 回复于 2020年03月08日 · 11867 次阅读

本帖已被管理员设置为精华贴

LRU

LRU(Least Recently Used) 是一种使用广泛的缓存数据替换策略，目的是在有限的内存空间中尽可能保留最有价值的缓存数据。其核心本意是，在资源出现不足时，剔除掉最近最少使用的数据，为新数据提供存放空间。

LRU 的使用场景非常之多，以最为常见的 MySQL 为例。由于磁盘 IO 的读取效率远远低于内存操作，这使得数据库倾向于将大量数据直接加载在内存中进行操作，极力减少磁盘读取的次数。

MySQL 中的 BufferPool 就是为此设计，但是内存的容量是远远小于磁盘容量，这使得只能加载部分数据到内存中，当 BufferPool 没有空闲的空间来缓冲新的数据时，就需要剔除部分数据，将空间让给看起来更有价值的数据。

而什么是更有价值的数据，该剔除哪些数据？LRU 的理念就是剔除掉最近使用最少使用的数据。 如果某份数据刚被使用，那么就认为它近期还可能被使用，且使用概率大于相对旧的数据，这和计算机的时间局部性内涵一致。最近最少使用的数据，应该为最近较多使用的数据让出空间。

概括来讲，LRU 是在资源有限的情况下，高效使用资源的一种策略，而这个策略的根基就是局部性原理。

LRU 实现

LRU 基于时间局部性进行数据淘汰，它用一个链表来追踪数据的时间局部性，当一份数据当下被访问了，就将该数据移动到链表的头部，链表从头到尾的顺序，相当于按照最近的访问时间对数据排序。当需要淘汰数据时，就将链表尾部的数据直接剔除，将需要新加入的数据插入链表的头部。

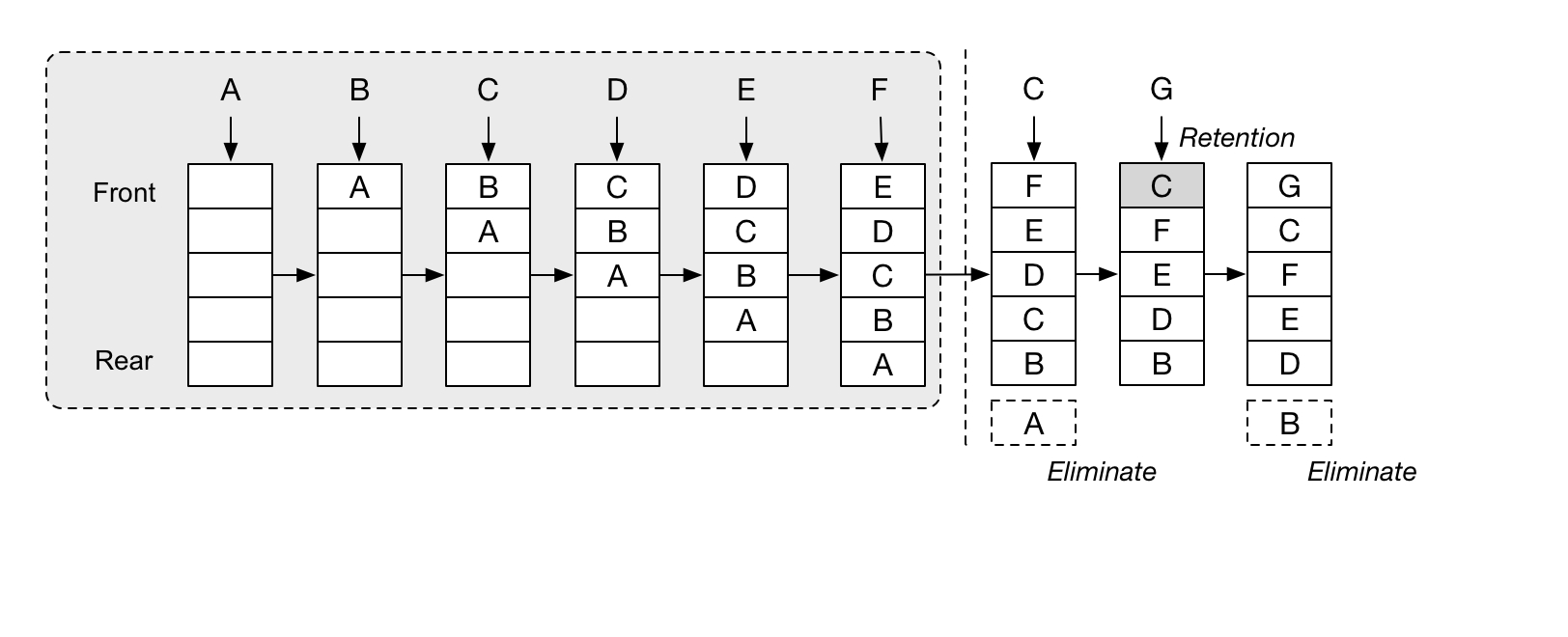
一个双向链表+HashMap 可以让 LRU 只有 O(1) 的时间复杂度，非常简单粗暴。而简单粗暴往往不能适应复杂的场景。

常规的数据访问规律可以分为以下几种：

顺序访问。所有的块一个接一个被访问，几乎不存在重访问。
循环访问。所有块都按照一定的间隔重复访问。
时间密集访问。最近被访问的块在将来可能被连续重复访问。
概率访问。所有块都有固定的访问概率，所有块都互相独立地根据概率被访问。

真实的环境是多种规律混杂，好的缓存替换算法需要有良好的适应性，LRU 在连续重复访问的模式下表现很好，但其他场景则较差，回到上文 MySQL 的场景。

当数据库对某个表进行一次全表扫描时，假设这个表的大小和 BufferPool 一样大，按照 LRU 的粗暴，表中的数据会顶掉其他数据，占满 BufferPool。如果扫描是偶发性的，那么 BufferPool 中相当于缓存的是无用的数据，被顶替掉的可能还是正在被高频访问的数据。

从上可以看出 LRU 的核心缺陷是：冷数据可以顶掉热数据，数据的替换策略并未考虑数据的冷热程度，只按照新近访问时间作为淘汰依据。在偶发性的扫描场景下，会让冷数据污染缓冲区，使得效率下降。

针对 LRU 的这种缺点，LFU(Least Frequently Used) 算法会追踪数据的访问频率，选择访问次数最低的进行淘汰，这种想法很好的考虑了数据真实的局部性，如果一个数据在最近一段时间内使用次数很少，那么在将来一段时间内被使用的可能性也很小，这种淘汰策略更加贴近真实的使用场景。不过这种策略不能够即时的跟上新的热点变化，老数据占的坑不能快速地移交给新的热点，在适应性上较差。

随之而来的是 2Q 算法，它其实是 LRU-K 的改良，能较好的解决上面 LRU 的问题。2Q 有一个 FIFO 队列用于放冷数据，一个 LRU 用来放热数据，将冷热数据区分对待，思想类似分代 GC 将新老对象区别处理。2Q 将第一次访问的冷数据放在 FIFO 队列中，当队列数据被再次访问 (在 FIFO 中命中) 时，将其视为热数据，放到 LRU 队列中进行管理。相当于用一个 FIFO 队列作为前置缓冲过滤掉突发性的冷数据，这样便解决了 LRU 的问题。不过随之而来的问题是 FIFO 队列的大小问题，如果太小则有些数据来不及提升为热数据就可能被移除 FIFO，如果太大则会过多占用有限的空间，其比例需要根据情况进行配置。

LIRS 则尝试在解决 LRU 问题基础上，让解决方案可能简单高效，同时具有较强的适应性。

LIRS

LIRS 继承了 LRU 根据时间局部性对冷热数据进行预测，在此之上 LIRS 引入了两个衡量数据块的指标：

IRR(Inter-Reference Recency) 页面最近连续两次块访问之间访问其他块的个数
R (Recency）页面最近一次访问到当前时间内访问其他块的个数，也就是 LRU 的维护的数据

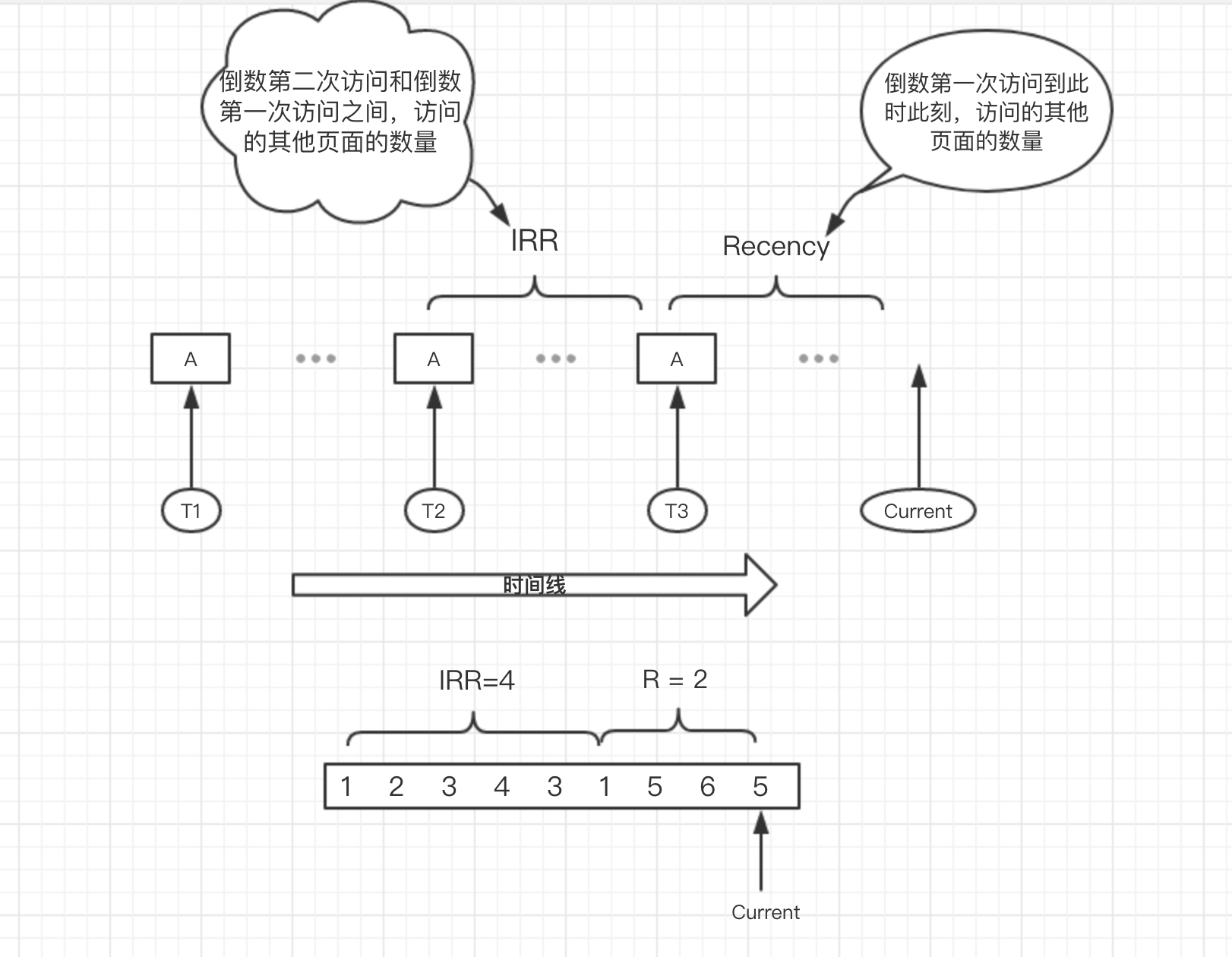
在图上的访问时间区间中：

数据 1: IRR=3(重复的块不算，上图总共有 4 次)，R=2
数据 5: IRR=1，R=0
而只访问了一次的 4：IRR 为无穷大，R=4

可以看出 IRR 是由 R 值计算而来，是历史信息的产物，在上图 current 时刻命中了一次“5“，其当前时刻的 R=0，IRR=上一时刻的R-当前时刻的R = 1 。

IRR 可以衡量数据当前访问的频度，IRR 越高说明在某个时间区间中，该数据的热度较低。而 LIRS 假设如果当前一个块的 IRR 比较大，那么该块的下一个 IRR 也会比较大，在进行数据淘汰时会优先选择 IRR 大的进行。

根据 IRR 值，LIRS 将数据块分为两种：

LIR，低 IRR 值，热数据
HIR，高 IRR 值，冷数据，接下来有可能成为热数据

LIRS 要做的就是用简单的方式动态地维护 IRR 和 R 值，让冷数据有机会成为热数据，而将变冷的热数据剔除出缓存，同时要避免 LRU 的弊端。

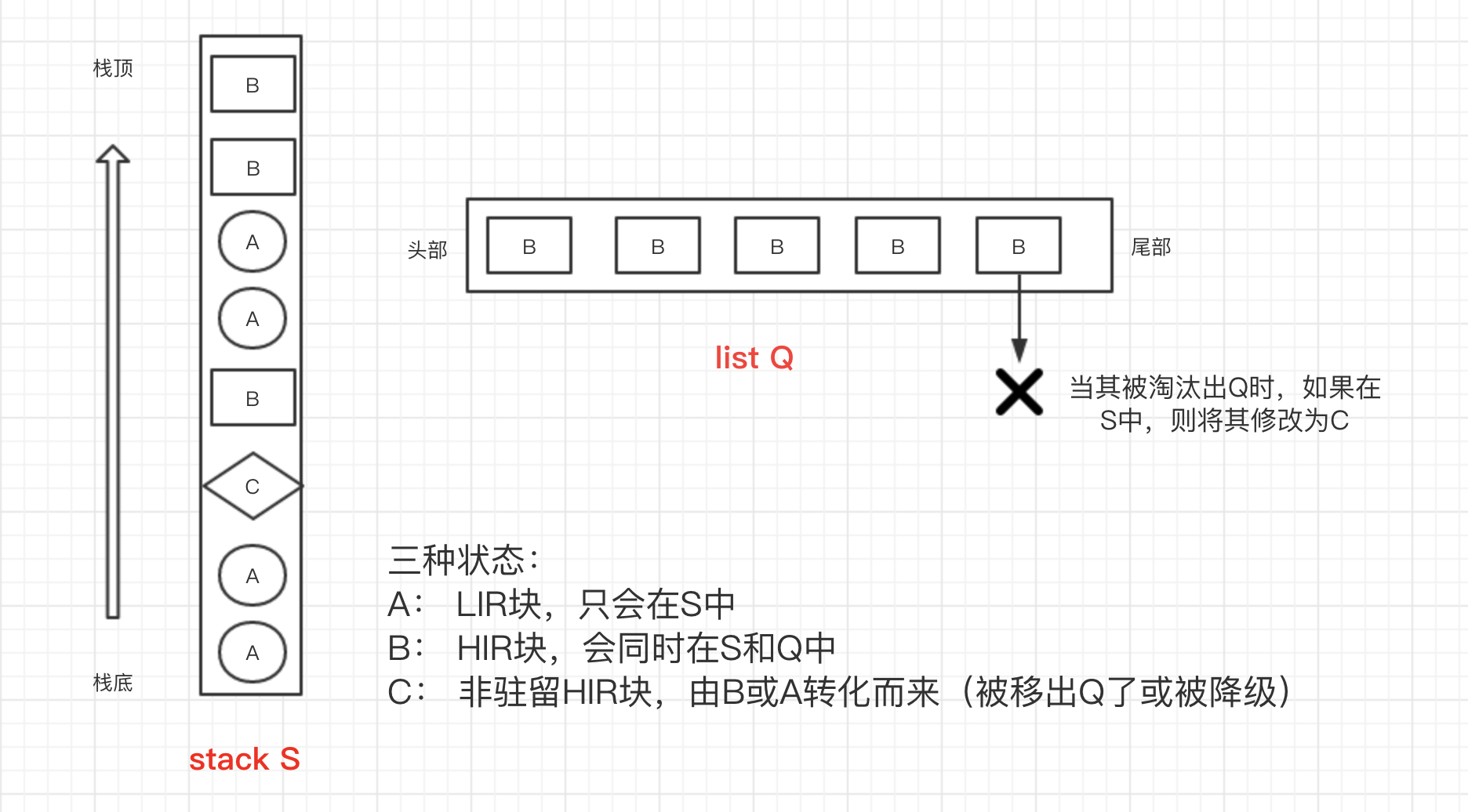
LIRS 通过一个栈 S 和一个队列 Q 来实现：

当缓存空间还没满时，所有的数据块都为 LIR，直接写入 S（S 的初始化）
当 LIR 数据块在 S 中被命中时，将块移动到 S 的顶部（维护 R 值）
当 LIR 的数量到达上限时，新加入的数据块为 HIR，同时写入 S 和 Q 的头部（R 值为 0）
当 Q 的空间不足时，则剔除 Q 尾部的数据，如果数据在 S 中，则将数据块设为非驻留 HIR 块，如果不在 S 中，则将数据测地剔除
HIR 被命中时，将其提升为 LIR 并移动到 S 顶部，如果存在于 Q 中，则将其从 Q 中剔除。将 S 底部的 LIR 剔除出 S（需要进行栈剪枝），降级为非驻留 HIR，写入 Q 的头部 (如果没能及时被再次访问会被彻底剔除)。

数据块在 S 中的位置就是 R 值，新数据和被命中的 LIR 块写入 S 头部就是为了动态维护 R 值，当一个 HIR 块提升为 LIR 时，需要淘汰一个 LIR 块，上文说了淘汰的策略是对比 IRR 值，当某个 HIR 的 IRR 值小于某个 LIR 的 IRR 值时，则将这两个数据块的状态互换。LIRS 抽象的点在于并没有看到 IRR 被维护，也就无法进行对比，这也是其设计的巧妙之处。

IRR 是由 R 值计算得出，具体的计算方式上文有提及： 上一个R值 - 命中时的R值(0)，当一个块被命中时，其 IRR 值也就立即刷新。要对比 IRR 值其实可以通过对比 R 值来实现，如果一个 HIR 块的 R 值小于某个 LIR 块的 R 值，那么当这个 HIR 块被命中时，其 IRR 值肯定小于这个 LIR 块的下一个 IRR 值。所以剔除 LIR 时简单的比较 R 值就行，这也是上面剔除逻辑中，直接剔除 S 底部的 LIR 的原因，因为 S 底部的 LIR 其 R 值最大。

当剔除 S 底部的 LIR(或底部 LIR 命中后移动到 S 顶部) 后，S 底部的数据块可能是 HIR 块，在 LIRS 的设定中要将底部的 HIR 块也移除出 S，保持 S 底部始终是 LIR，这被称为栈剪枝。进行栈剪枝的目的在我看来是为了维护 HIR 块和 LIR 块之间 IRR 值比较的环境，用热的 HIR 去顶掉最老的 LIR，S 底部的 HIR 显得突兀需要移除，其 IRR 本身也很大，且因为没有 LIR 可比较，没有机会变成 LIR。

从数据访问的角度来描述以下算法细节：

数据块不存在于缓存中。为该数据分配空间，并写入 Q 的头部，写入 S 的头部。如果 Q 空间满了，则剔除掉 Q 尾部的数据块，如果数据块也在 S 中，则将其状态改为非驻留 HIR，不然彻底移出缓存。如果 S 的空间到达上限，则移除 S 底部的 HIR，写入 Q 的头部。
如果访问的是 LIR，则将 LIR 块移动到 S 头部，如果 LIR 位于 S 底部，则需要栈剪枝
如果访问的是 HIR，则分为几种情况：
- 如果 HIR 同时存在于 S 和 Q 中，则将 HIR 块提升为 LIR，从 Q 中移除，将 S 底部的 LIR 降级为 HIR，写入 Q 的头部，需要栈剪枝
- 如果 HIR 只在于 Q 中，则将保持其 HIR 状态，并写入 S 顶部，移到 Q 头部
- 如果 HIR 只位于 S 中，则将其提升为 LIR，移入 S 顶部，将 S 底部 LIR 剔除，移入 Q 顶部，需要栈剪枝

LIRS 中没有对 S 的大小进行限制，这在极端情况下会导致 S 大小不可控，弥补措施是给一个最大数量限制，当超过限制时，往 S 中写入一个数据之前要先剔除一个 S 底部的 HIR 块。

深感水平有限，未能以让自己满意的程度完成本文，后续待恶补。LIRS 的难度适中，实现的过程充满乐趣，如果你正在繁琐的搬砖开发中陷入枯燥迷惘，根据论文实现一遍 LIRS 是个不错的选择。