Web 开发会经常遇到给实体打分的需求,比如论坛用户的声望分、电商系统的类目和产品热度分,新闻的热度分等。有些分数只需要排序使用,有些分数需要显示给用户,让用户看到分数之后能直观的感受到这个分数所处的位置。往往热度分的计算并不只是参考单一维度,会有很多维度的参考。比如,如果我们想计算一个论坛的用户的综合贡献值,需要参考回帖数量、发帖数量、被点赞数量等指标。下面以论坛用户贡献值为例子来演示一个热度分的计算过程。
首先,初始化一个用户表,200 条记录,字段为id,post_count, reply_count, faver_count,值为随机整数。
SELECT row_number() over() as id,
(generate_series * random())::integer as post_count,
(generate_series * random())::integer as reply_count,
(generate_series * random())::integer as faver_count
INTO TABLE users
FROM (SELECT * FROM generate_series(1, 200)) AS r;
users表数据如下:
select * from users limit 10;
id | post_count | reply_count | faver_count
----+------------+-------------+-------------
1 | 0 | 0 | 0
2 | 2 | 1 | 1
3 | 2 | 2 | 1
4 | 3 | 0 | 1
5 | 3 | 3 | 4
6 | 4 | 3 | 3
7 | 4 | 0 | 3
8 | 5 | 4 | 3
9 | 7 | 2 | 5
10 | 6 | 3 | 5
Row Number
最简单的想法是单指标的排名相加,比如,按post_count从大到小排序,算出post_num,reply和faver同理:
SELECT *,
row_number() over(order by post_count desc) as post_num,
row_number() over(order by reply_count desc) as reply_num,
row_number() over(order by faver_count desc) as faver_num
FROM users;
计算结果如下,score = a * post_num + b * reply_num + c * faver_num,其中abc为加权系数。这样的计算方法存在一个问题,score的范围不确定,一个用户打了 99 分的话,我们无法从 99 这个数值看出他处于什么位置。
id | post_count | reply_count | faver_count | post_num | reply_num | faver_num
-----+------------+-------------+-------------+----------+-----------+-----------
187 | 62 | 25 | 173 | 70 | 122 | 1
169 | 6 | 57 | 167 | 176 | 69 | 2
171 | 2 | 46 | 162 | 193 | 84 | 3
172 | 41 | 152 | 162 | 101 | 6 | 4
200 | 76 | 193 | 149 | 51 | 1 | 5
156 | 62 | 116 | 144 | 69 | 28 | 6
166 | 114 | 31 | 144 | 20 | 109 | 7
153 | 127 | 97 | 138 | 10 | 39 | 8
135 | 25 | 131 | 135 | 135 | 16 | 9
186 | 112 | 147 | 134 | 23 | 7 | 10
163 | 106 | 134 | 133 | 28 | 13 | 11
155 | 124 | 3 | 132 | 14 | 188 | 12
173 | 74 | 92 | 132 | 53 | 42 | 13
133 | 119 | 78 | 132 | 17 | 53 | 14
NTile
一个改进的方案是,排名之后按区间分段,比如 1-10 打 1 分,11-20 打 2 分,以此类推。这样可以把每个指标的范围确定,再加权之后范围也是可以计算的。
SELECT *,
ntile(10) over(order by post_count desc) as post_num,
ntile(10) over(order by reply_count desc) as reply_num,
ntile(10) over(order by faver_count desc) as faver_num
FROM users;
按区间分段存在的问题是,结果不够平滑,也不能反映不同用户之间的差别,比如第一名和第二名分别为 10000 和 100,分段之后他们得到相同的分数,体现不出差异。
id | post_count | reply_count | faver_count | post_num | reply_num | faver_num
-----+------------+-------------+-------------+----------+-----------+-----------
187 | 62 | 25 | 173 | 4 | 7 | 1
169 | 6 | 57 | 167 | 9 | 4 | 1
171 | 2 | 46 | 162 | 10 | 5 | 1
172 | 41 | 152 | 162 | 6 | 1 | 1
200 | 76 | 193 | 149 | 3 | 1 | 1
156 | 62 | 116 | 144 | 4 | 2 | 1
166 | 114 | 31 | 144 | 1 | 6 | 1
153 | 127 | 97 | 138 | 1 | 2 | 1
135 | 25 | 131 | 135 | 7 | 1 | 1
186 | 112 | 147 | 134 | 2 | 1 | 1
163 | 106 | 134 | 133 | 2 | 1 | 1
155 | 124 | 3 | 132 | 1 | 10 | 1
173 | 74 | 92 | 132 | 3 | 3 | 1
133 | 119 | 78 | 132 | 1 | 3 | 1
174 | 42 | 14 | 131 | 5 | 8 | 1
181 | 120 | 10 | 130 | 1 | 8 | 1
148 | 38 | 120 | 129 | 6 | 2 | 1
176 | 84 | 105 | 128 | 3 | 2 | 1
128 | 113 | 103 | 128 | 2 | 2 | 1
179 | 114 | 118 | 127 | 1 | 2 | 1
157 | 66 | 120 | 127 | 4 | 2 | 2
198 | 122 | 35 | 126 | 1 | 6 | 2
195 | 166 | 112 | 118 | 1 | 2 | 2
192 | 175 | 124 | 117 | 1 | 1 | 2
Z Score
标准分数(Standard Score,又称 z-score,中文称为 Z-分数或标准化值)在统计学中是一种无因次值,就是一种纯数字标记,是借由从单一(原始)分数中减去母体的平均值,再依照母体(母集合)的标准差分割成不同的差距,按照 z 值公式,各个样本在经过转换后,通常在正、负五到六之间不等。

WITH post AS (SELECT avg(post_count) as mean, stddev(post_count) as sd from users),
reply AS (SELECT avg(reply_count) as mean, stddev(reply_count) as sd from users),
faver AS (SELECT avg(faver_count) as mean, stddev(faver_count) as sd from users)
SELECT users.*,
((post_count - post.mean) / post.sd)::numeric(6,3) AS z_score_post,
((reply_count - reply.mean) / reply.sd)::numeric(6,3) AS z_score_reply,
((faver_count - faver.mean) / faver.sd)::numeric(6,3) AS z_score_faver
FROM users,
post,
faver,
reply
ORDER BY 4 DESC
结果如下:
id | post_count | reply_count | faver_count | z_score_post | z_score_reply | z_score_faver
-----+------------+-------------+-------------+--------------+---------------+---------------
187 | 62 | 25 | 173 | 0.251 | -0.543 | 2.835
169 | 6 | 57 | 167 | -1.076 | 0.150 | 2.697
172 | 41 | 152 | 162 | -0.247 | 2.208 | 2.582
171 | 2 | 46 | 162 | -1.171 | -0.088 | 2.582
200 | 76 | 193 | 149 | 0.582 | 3.096 | 2.283
156 | 62 | 116 | 144 | 0.251 | 1.428 | 2.168
166 | 114 | 31 | 144 | 1.483 | -0.413 | 2.168
153 | 127 | 97 | 138 | 1.791 | 1.016 | 2.031
135 | 25 | 131 | 135 | -0.626 | 1.753 | 1.962
186 | 112 | 147 | 134 | 1.435 | 2.099 | 1.939
163 | 106 | 134 | 133 | 1.293 | 1.818 | 1.916
133 | 119 | 78 | 132 | 1.601 | 0.605 | 1.893
173 | 74 | 92 | 132 | 0.535 | 0.908 | 1.893
155 | 124 | 3 | 132 | 1.720 | -1.019 | 1.893
174 | 42 | 14 | 131 | -0.223 | -0.781 | 1.870
181 | 120 | 10 | 130 | 1.625 | -0.868 | 1.847
148 | 38 | 120 | 129 | -0.318 | 1.515 | 1.824
128 | 113 | 103 | 128 | 1.459 | 1.146 | 1.801
176 | 84 | 105 | 128 | 0.772 | 1.190 | 1.801
179 | 114 | 118 | 127 | 1.483 | 1.471 | 1.778
Z-Score的意义是样本值到均值之间有多少个标准差,它的取值理论上也是没有范围的,但如果样本数值服从正态分布,会有 99% 以上的值落在 [-3, 3] 这个区间。如图:
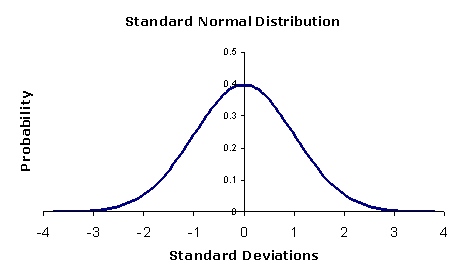
其实从上面我们计算的结果也可以观察出这个结论。对于落在[-3, 3]区间外的数据,我们可以调整为 3 或 -3,这个影响完全可以忽略不计。使用Z-Score之后,我们可以保证了分数值既平滑又有范围区间。