Dijkstra 大学的时候就学过，但最近在 [《Algorithms》][1] 这本书里，看到了个很有趣的讲解，对这个算法有了新的理解，以下便是对这个算法的整理和实现。

广度搜索与最短距离

我们知道，如果把所有的边的距离当做 1，广度遍历得到的就是最短路径。

更直观的，我们可以这样想，把节点都想成有质量的小球，节点间边想成细线。我们把 S 球拎起来，让所有的球都自然下垂，这样小球所在的层数，就是 S 球到其他小球的最短距离了。如下图：

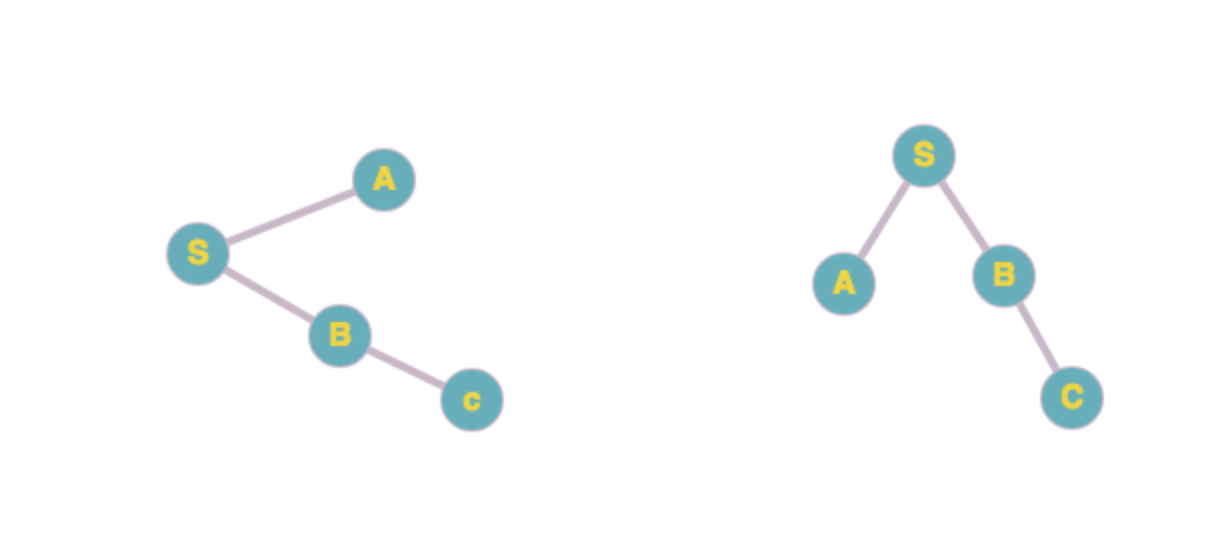
我们可以简单证明下。

首先，广度搜索，又被称为层次遍历，就是一层一层进行搜索。当搜索到 d 层，所有小于 d 层的节点一定已经搜索完了。

假设在某一个时刻，所有 d 层的节点都已经计算正确了。那么他们相邻的节点的距离只有两种情况，一种是未知的，那么他们同 S 的最短距离应为 d + 1。

一种是已知的，距离小于等于 d，根据假设，他的距离也已经计算正确了。

然后，我们再考虑初始情况。S 节点的距离为 0，相邻的节点距离都为 1，符合我们的假设。所以通过广度搜索得到的距离是最短距离。

这个"证明"只是用来理解这个算法的，并不去严谨，《[算法导论][3]》有严谨的证明，大家感兴趣的话可以去看看。

广度搜索到 Dijkstra

既然我们知道广度搜索能得到所有边的距离为 1 的节点的最短距离了。那么广度搜索和 Dijkstra 有没有什么关系呢？换句话说，最短路径能不能变成广度搜索呢？

最短路径和广度搜索的区别就在于，广度遍历之间的节点距离只能为 1，而最短路径计算的节点距离可以为任意正数。

如果我们把所有距离都变成1 会怎样？

为了达到这个目的，我们把两个几点之间加上如果哑节点（dummy node），让所有节点（节点 + 哑几点）间的距离为 1，这样我们就可以用广度遍历来算最短距离了！

比如 s 同 u 的距离为 3，那么我们可以在 S 和 U 之间加上两个节点 u1 ,u2。这样就变成了 S -> U1 -> U2 -> U，相邻的节点间的距离为 1。如下图：

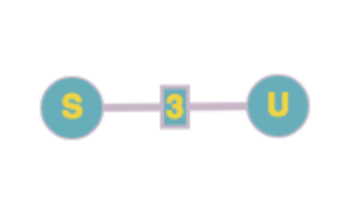
目前的算法看起来有点蠢，不过已经很接近 Dijkstra 了。我们看下如何来优化它！

优化当前的算法吗

算法好玩的地方就在于，我们可以优化它。

首先，我们先分析这个算法的问题。

假设从 S 到 U 的距离是 100，那么计算前 99 个哑节点的距离，都是没有意义的。

如果我们在 90 分钟里，睡一下，在第一百分钟的时候，有一个闹铃把我们叫醒，就好了！让我们来做这样的一个闹铃！

假设我们要求下图的的最短距离，我们可以这么做。我们从 0 出发，从图中可以看出来，直到 100 或者 200 分钟后，不会有任何有趣的事情发生。那我们就设两个闹铃，分别为 100 分钟、200 分钟之后响。

等到 100 这个闹铃响的时候，我们到了 1 号节点，这个时候，我们检查 1 号节点的相邻节点，发现 50 分钟后，可能会到 2 号节点。所以我们加入 150 这个闹铃。

150 分钟到的时候，我们到了 2 号节点，所以 2 号的最短距离是 150。这样就得到了所有节点的最短距离。

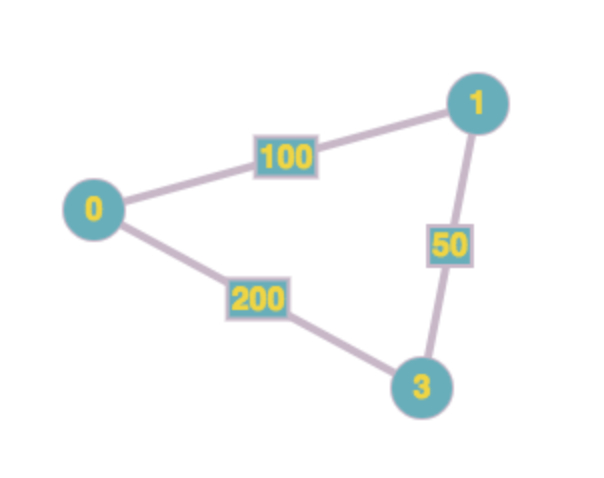
我们的闹钟算法如下：

• 讲 S 的闹钟设为 0
• 循环，直到没有任何一个闹钟 假设，下一个闹钟 (距离最近的节点) 响起响起的时间是 T，到达的节点是 U，那么
  • 从 S 到 U 的距离就是 T
  • 对于 U 的每一个相邻节点 V
    • 如果 v 还没有闹钟，则将它的闹钟设置为 T + l(u, v)
    • 如果 v 的闹钟，比 T + l(u,v) 晚，则更新 v 的闹钟

Dijkstra 实现

我们来看下具体实现，实现算法可以帮助我们进一步理解算法。

class Dijkstra
  INFINITY = 1 << 32
  def initialize(weighted_graph)
    @weighted_graph = weighted_graph
  end

  def shortest_distances
    make_alarms
    decrease_alarm(0, 0)

    while v = alarm!
      @weighted_graph[v].each do |w, weight|
        if alarm(w) > alarm(v) + weight
          decrease_alarm(w, alarm(v) + weight)
        end
      end
    end

    @alarms
  end

  def make_alarms
    @vertexes_alarms = (0...vertexes_count).to_a

    @alarms = Array.new(vertexes_count, INFINITY)
  end

  def alarm(vertex)
    @alarms[vertex]
  end

  def decrease_alarm(vertex, time)
    @alarms[vertex] = time

    @vertexes_alarms.sort_by! do |vertex|
      @alarms[vertex]
    end
  end

  def alarm!
    @vertexes_alarms.delete_at(0)
  end

  def vertexes_count
    @vertexes_count ||= @weighted_graph.length
  end
end

优化

自己观察这个算法，会发现decrease_alarm这个方法，每次都调用了sort!方法。但其实我们每次拿出来的闹铃都是数值最小的那一个，用优先队列 (Priority queue) 更合适。这样可以降低算法的复杂度，让我们的算法更快。

总结

算法的书有很多，但讲清楚算法是怎么来的，却很少。《Algorithms》这本书采用的方式，很像《怎样解题》所采用方式，很有趣，也很有启发性。

同时算法最有趣的地方在于可以一点一点改进和优化！

原文链接

参考

1. [Algorithms][7]
2. [算法导论][8]
3. [怎样解题][9]
4. [画图网站][10]

[1]: https://book.douban.com/subject/1996256/ [2]: /img/bVIIAM [3]: https://book.douban.com/subject/1885170/ [4]: /img/bVIIA8 [5]: /img/bVIIBb [6]: /img/bVIIBP [7]: https://book.douban.com/subject/1996256/ [8]: https://book.douban.com/subject/1885170/ [9]: https://book.douban.com/subject/2124114/ [10]: http://graphonline.ru/en/