在Haskell 的网站上看到了一道数独的题目，和一系列不同的解法。

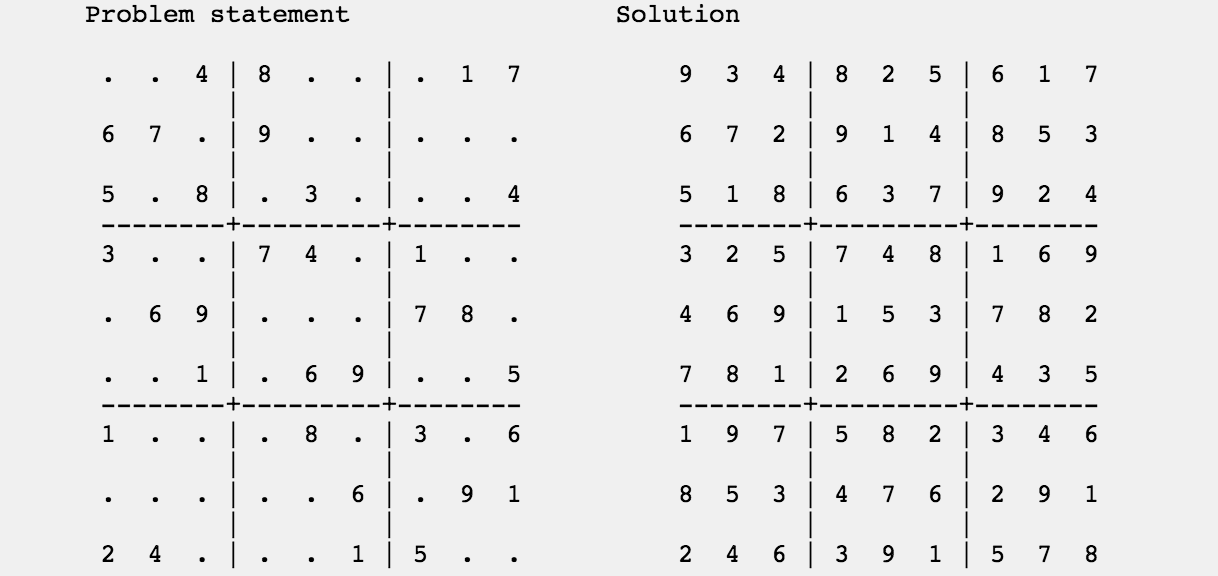
其中最精简的一个解法是这样的：

Module Main where f x s@(h:y)=let(r,c)=divMod(length x)9;m#n=mdiv3==ndiv3;e=[0..8]in [a|z<-['1'..'9'],h==z||h=='.'&& notElem z(map((x++s)!!)[i*9+j|i<-e, j<-e,i==r||j==c||i#r&&j#c]),a<-f(x++[z])y] f x[]=[x] main=print$f[]"53..7....6..195....98....6.8...6...34..8.3..17...2...6.6....28....419..5....8..79"

原始链接在此

这份代码可以先不着急读，后面会详细讲解。

这个解法代码非常少，其实算法也是普通的回溯法。具体来说就是从前到后检查所有没填数字的位置，排除与这个数字同一行、同一列、及处在同一个块中的所有数字，然后从剩下的数字中挑选一个填上去，再对下一个没填数字的位置做相同的操作，直到把棋盘上所有的位置都填完。如果在某个位置上找不到可用的数字，则回溯到上一个位置，尝试下一个可能的数字。

使用 ruby 写出来的代码可以是这样的：

BLOCK_SIZE = 3
PANEL_SIZE = BLOCK_SIZE * BLOCK_SIZE

def nums_in_row(panel, index)
  row_start = (index / PANEL_SIZE) * PANEL_SIZE
  panel[row_start..row_start + PANEL_SIZE - 1]
end

def nums_in_column(panel, index)
  column = index % PANEL_SIZE
  (0..PANEL_SIZE - 1).map{|row| panel[row * PANEL_SIZE + column]}
end

def nums_in_block(panel, index)
  block_row = index / PANEL_SIZE / BLOCK_SIZE
  block_column = index % PANEL_SIZE / BLOCK_SIZE

  nums = []

  (0..BLOCK_SIZE - 1).each do |block_i|
    (0..BLOCK_SIZE - 1).each do |block_j|
      row = block_row * BLOCK_SIZE + block_i
      column = block_column * BLOCK_SIZE + block_j
      nums << panel[row * PANEL_SIZE + column]
    end
  end
  nums
end

def all_possible_next(state)
  target_index = state.index 0
  used_nums = (nums_in_row(state, target_index) +
                nums_in_column(state, target_index) +
                nums_in_block(state, target_index)).uniq
  ((1..PANEL_SIZE).to_a - used_nums - [0]).map do |num|
    cloned = state.clone
    cloned[target_index] = num
    cloned
  end
end

def all_filled?(state)
  state.none?{|num| num == 0}
end

def solve(original)
  stack = []
  stack.push original

  solutions = []

  until stack.empty?
    current = stack.pop
    all_possible_next(current).each do |state|
      if all_filled? state
        solutions << state
      else
        stack.push state
      end
    end
  end
  solutions
end

代码量上差距巨大！那为什么用 Haskell 可以写的这么简洁呢，其中一个很重要的原因已经写在这道题答案的 url 中了，它使用了 List Comprehension。

原始的代码变量名比较随意，不太好读，我把它稍微重构了一下，如下：

module Main where
f :: [Char] -> [Char] -> [[Char]]
f x s@(h:y)=let (row,column)=divMod (length x) 9
                inSameSegment m n = m`div`3==n`div`3
                availNums=[0..8]
                inSameBlock x1 y1 x2 y2 = inSameSegment x1 x2 && inSameSegment y1 y2
                usedNums = map((x++s)!!)[i*9+j|i<-availNums,j<-availNums,i==row||j==column||inSameBlock i j row column]
            in
              [a|z<-['1'..'9'], h /= '.' || h=='.' && notElem z (usedNums), a <- f (x++[z]) y]
f x []=[x]

main=print $ f [] "53..7....6..195....98....6.8...6...34..8.3..17...2...6.6....28....419..5....8..79"

其中这部分

[i*9+j|i<-availNums,j<-availNums,i==row||j==column||inSameBlock i j row column]

就是一个典型的 list comprehension。 这个表达式返回的是一个数组（Haskell 中其实叫列表） 它的计算过程是：i 和 j 分别可以是 availNums 这个数组中的任意元素，如果 i 和 j 的某个组合满足这个条件

i==row||j==column||inSameBlock i j row column

那么 i*9+j 就会成为最终返回的数组中的一个元素。 对于这个例子，可以简单的理解为一个两重循环，像这样：

result = []
availNums.each do |i|
  availNums.each do |j|
    if i==row||j==column||inSameBlock(i, j, row, column)
      result << i*9+j
    end
  end
end

直接写两重循环还可以忍受，但是如果再深就没法看了。但是使用 list comprehension 就还好，因为多余的元素足够少。 那么好吧，就让我们实现一个 ruby 的 list comprehension 吧。

def lc_internal(lists, params, condition_proc, result_proc)
  l = lists.first
  if l.nil?
    case params.size
      when 1
        if condition_proc.call params[0]
          [(result_proc.call params[0])]
        end
      when 2
        if condition_proc.call params[0], params[1]
          [(result_proc.call params[0], params[1])]
        end
      else
        raise 'only support at most 2 list'
    end
  else
    l.map do |ele|
      vals = lc_internal lists[1..-1], params + [ele], condition_proc, result_proc
      vals.nil? ? [] : vals
    end.reduce(:+)
  end
end

def list_comprehension(*lists, condition_proc, result_proc)
  lists.first.map do |ele|
    lc_internal lists[1..-1], [ele], condition_proc, result_proc
  end.reduce(:+)
end

其中向外暴漏的是 list_comprehension，它包含了三个参数，第一个参数可以接受多个数组；第二个参数是个 Proc，用来判断某个组合是否满足指定的条件；第三个参数也是个 Proc，使用这个组合来计算出相应的值，这个值，如前面提到的，会成为最终返回数组中的一个元素。 关于“如何把一个数组传递给多个参数的函数这件事情”，不知道怎么做，所以写了一个丑陋的 case 语句，目前只能支持两个列表，多了就报错了！

然后再回到第一个版本的 ruby 代码，使用 list_comprehension 之后，主要变化的地方就是 all_possible_next 这个函数，现在这个函数变成这样了：

def all_possible_next(state)
  avail_nums = (0..PANEL_SIZE - 1).to_a

  target_index = state.index 0
  row = target_index / PANEL_SIZE
  column = target_index % PANEL_SIZE
  used_nums = list_comprehension(avail_nums, avail_nums,
                               Proc.new{|i, j| i == row or j == column || (i / 3 == row / 3 && j / 3 == column / 3)},
                               Proc.new{|i, j| state[i*9+j]}).uniq
  ((1..PANEL_SIZE).to_a - used_nums).map do |num|
    cloned = state.clone
    cloned[target_index] = num
    cloned
  end
end

当然了，原来版本中的前三个函数也都不需要了。原来的 63 行代码变成现在 43 行了，少了 1/3。 这份 ruby 代码可以继续优化，不过本文就到此为止了。

函数式编程中真是有不少好东西，可以借鉴到其他语言中用。